Географические координаты Алматы (широта и долгота)

Для чего нужны координаты?

Отец у меня был геодезистом, у него в кабинете висела карта мира, а на столе лежал маленький глобус. Я проводил большую часть своего времени, изучая их. Меня очень интересовали маленькие цифры, которые мне удалось обнаружить. Но только в школе я смог узнать, что это координаты.

Что такое координаты

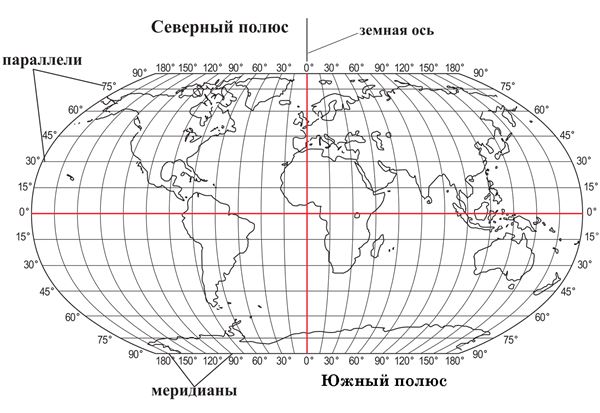
Человечество ещё давным-давно научилось ориентироваться в пространстве. Это могли быть: мох, горы, леса и т. п. Они оставляли ориентиры: рисунки, обозначения. Потом появились карта, глобус, навигатор. Посмотрев на них, вы сразу увидите вертикальные и горизонтальные линии, что пересекаются и создают квадраты. Эти линии — параллели и меридианы. Каждый квадрат имеет долготу и широту. Для наглядности возьмите глобус.

Широта, долгота, глубина и высота — координаты, определяющие нахождение точки на Земле.

Координаты — числа, величины, что обозначают место положения объекта в пространстве.

Где используются координаты

Сегодня использование координат в повседневной жизни не имеют большого значения, навигатор сможет доставить в точку назначения без лишних усилий и знаний, но в других, более сложных областях, координаты играют великую роль.

Приведу лишь несколько примеров, так как их очень много, перечисление заберёт очень большое количество времени.

• Топография.
• Математика.
• Компьютерные приложения для дизайна и моделирования.
• Геодезия.

В топографии и геодезии координаты имеют широкое использование. С их помощью создаются топографические карты, вычисляется территория, измеряется ширина и длина местности.

В математике вычисляют размеры фигур. Векторы, гиперболы тоже имеют свои координаты — (x; y), которые нашли своё применение и в моделировании.

Виды координат

Поскольку координаты встречаются в разных областях, то их решили поделить на такие виды:

• географические координаты;
• геодезические координаты;
• геоцентрические координаты;
• плоские прямоугольные координаты;
• пространственные прямоугольные координаты;
• полярные координаты;
• биполярные координаты.

Друзья, вы часто спрашиваете, поэтому напоминаем!

Авиабилеты — сравнить цены от всех авиакомпаний и агентств можно тут!

Отели — не забываем проверять цены от всех сайтов бронирования! Не переплачивайте. Это тут!

Аренда авто — тоже агрегация цен от всех прокатчиков, все в одном месте, идем сюда!

Моё знакомство с географическими координатами произошло ещё в школе. Правда, тогда мне казалось, что это абсолютно бесполезная информация. Но я очень сильно ошибался. Как-то раз я поехал на машине в путешествие. У автомобиля как назло лопнуло колесо. Указателей или близлежащих поселений там не было. Позвонив другу, я не смог даже примерно описать, где нахожусь. В той ситуации меня спас навигатор, а точнее точные географические координаты моего местоположения.

Для чего понадобились географические координаты

В повседневной жизни географические координаты, как правило, совершенно бесполезная вещь. Но отправляясь в поездку своим ходом, вы пользуетесь навигатором или картой. Очевидно, что карта появилась значительно раньше навигатора. Составляя карту, древние люди задавались вполне логичным вопросом. А как, глядя на карту, можно понять, в какую именно сторону нужно идти, чтобы попасть в определённое место? Без этой информации было бы невозможно покорять неизведанные края. Для решения проблемы было придумано разделить весь земной шар линиями, которые бы делили его на своеобразные квадратики. Таким образом, можно было понять, глядя на компас, в какую сторону двигаться. Правда, компас появился только в 13-м веке, а для определения сторон света, люди ориентировались по Солнцу.

Кому нужны географические координаты

Область применения географических координат достигает колоссальных размеров. Географические координаты используют:

Этот список очень большой. На перечисление всех видов деятельности, в которых используются географические координаты, элементарно не хватит времени.

Интересный факт о географических координатах

Оказывается, что не только на нашей планете есть широта и долгота. Астрономы позаботились и о других планетах нашей Солнечной системы. Они создали на тех планетах аналогичную систему координат, которая охватывает ещё и их сферы. Эта система координат потребовалась для различных астрономических исследований, а также активно применяется в космонавтике.

Как же часто я на уроках географии встречался с координатами. Также во многих играх мне приходилось их определять или просто наблюдать, как это делают герои. Поиск правильных координат также можно наблюдать и в фильмах. В общем, координаты являются очень важными, и необходимо знать про них, так как они могут пригодиться в реальной жизни.

Как в географии описываются координаты

Впервые каждый из нас узнал, что такое координаты, на уроках географии. Там мне ясно дали понять, что они нужны, чтобы не заблудиться в мире. С их помощью человек будет твердо знать, куда направляется и где находится на земном шаре в тот или иной момент. Чтобы их определить, необходимо уметь пользоваться картой или глобусом. На них, помимо материков, стран и городов, показаны цифры, которые особым образом располагаются по карте.

Расположение цифр выполняется по условным линиям. Их еще называют параллелями и медианами, которые показывают долготу и широту. Каждое место на планете имеет свою долготу и широту, которую можно определить по карте.

В географии Землю принято считать идеальной сферой, а не эллипсом. Сфера имеет угол в 360 градусов, поэтому на карте планета разделена на столько же условных линий. Планета крутится вокруг своей оси и имеет Северный и Южный полюса. Эти полюса указывают на долготу, и на планете существуют две важные такие линии. Одна называется нулевой, а вторая ─ 180 градусов.

Параллелями являются линии, которые показывают широту. Каждая линия широты расположена поперек вращения Земли вокруг своей оси. На экваторе располагается главная параллель, которая разделяет планету на 2 полушария, и в каждом насчитывается по 90 линий широты.

В географии градусы принято ещё делить на минуты и секунды.

Зачем нужны координаты

Мореплавателям приходится прибегать к помощи координат. Таким образом можно определить, где они находятся, чтобы выбрать правильный курс и не заблудится в морских или океанических водах.

Благодаря медианам и параллелям, наша планета для удобства поделена на следующие полушария:

Насколько я помню, теория относительности слабо рассматривается в школьном курсе физики. Поэтому большинство людей привыкло, что координаты местоположения предмета в пространстве всего лишь два, ну, может быть, три показателя. Но вот пришел Эйнштейн со своей теорией, и все стало немного сложнее, а кому-то – проще.

Координаты в системе пространство-время

Евклидово пространство, которое плотно изучают в школе, не привязано ко времени, и там нет такого понятия как событие, а существует система неподвижных тел с тремя координатами:

В теории относительности же введено понятие времени, и оно как бы идет параллельно с другими координатами.

С введением времени в пространстве появляется место событию, которым может быть изменение, перемещение, исчезновение тела. Таким образом, исходя из общих законов физики, время ограничивает существование тела в пространстве до момента перехода его энергии в другое состояние. Ведь известно, что энергия никуда не исчезает, а лишь меняет свою форму.

Координаты «летящей стрелы»

Эта апория (безысходность) была предложена древнегреческим философом Зеноном. Заключается она в том, что летящая стрела будет неподвижна в каждый отрезок времени, соответственно, координаты ее меняться не будут, поэтому относительно временного отрезка она двигаться не будет.

Предположить же, что если взять более мелкие периоды времени, то стрела все же будет двигаться — невозможно, т. к. дробление времени может быть бесконечным, и, соответственно, в каждом более мелком периоде стрела имеет постоянные координаты и не движется. Загвоздка состоит в том, что в природе нет физического эквивалента математическим понятиям времени.

Координаты при перемещении во времени

Вопрос хорошо отражен в теории Уэллса в «Машине времени». Если перемещаться относительно шкалы времени, то координаты предмета должны быть неподвижны.

Сам же предмет должен быть защищен особым полем, которое будет разрушать внешние объекты, которые могут находится в тех же 3-мерных координатах при перемещении путешествующего предмета.

Любой человек в мире имеет какие-то свои признаки для ориентации во времени, пространстве и так далее. Одним из таких признаков являются координаты, с помощью которых люди могут знать точное местоположение и не только. Но я задался в свое время вопросом, что такое эти координаты в научном понимании и какие они бывают.

Координаты в географии

По большей части, координаты используются все-таки в географии. Многие со школы помнят координатную ось и все тому подобное. Но это имеет узкую направленность, а именно – математическую. Координаты в географии же имеют более расширенный и важный смысл. Географические координаты можно назвать наследником астрономических и геодезических координат. То есть, это их обобщенное понятие. Для определения координат в географии указывают положение объекта на поверхности планеты. Такие же координаты можно применить и к другим планетам.

Широта, долгота и высота

Для точного и полного определения места нахождения той или иной точки, используются следующие три характеристики:

Эти три слова, думаю, слышал каждый. Ученые называются широту и долготу углами, которые проходят между экватором и направлением зенита и между нулевым меридианом и меридианом, проходящим через нужную нам точку соответственно. Если обратить внимание на широту, то в Северном полушарии она положительная, а в Южном, наоборот – отрицательная. Долгота, в свою очередь, делится на восточную и западную. Высота всегда берется для полного определения местоположения в трехмерном пространстве. В географии высота используя в качестве высоты над уровнем моря.

Применение координат в географии

Простыми словами из всего вышесказанного, географические координаты нужны для ориентации в пространстве или для навигации на какой-либо заданной местности. То есть, я могу знать координаты любого здания или города, или простого дерева, и тогда буду иметь возможность добраться до заданного места, имея навигатор.

В современных навигаторах все просто: вбил координаты места – и вперед!

Ответ на это вопрос для меня стал очевидным, когда я потерялся в таёжных лесах Сибири. Расскажу вам для чего нужны координаты, что это такое, и как я нашелся.

Необходимость координат

Координаты нужны для того, чтобы не потеряться или что-нибудь найти.

Координатами могут стать любые объекты или направления в пространстве. Например, мое место жительства – поселок Михайловский. Но такие поселки есть в каждой области России. Более точным будет указать область, например Московскую. Вы скажете: «В Московской области несколько таких поселков». Тогда нужно знать и район области. Например, Солнечногорский. Так, поселок вы уже нашли, но меня-то – нет. Меня нужно разыскать еще и в поселенке.

Область, район и поселок – это приблизительные, не точные координаты моего места пребывания. А вот знание географических координат поможет вам отыскать меня гораздо быстрее. Географические координаты указаны на полях любой мало-мальски точной карты региона и в современных телефонных устройствах, обрадованных системами навигации.

Географические координаты

Географические координаты – это числа, которые показывают ваше место в комнате, городе, стране или океане. Географические координаты определяются тремя параметрами:

1. Широта – изменение положения предмета в направлении от экватора к любому географическому полюсу. Широта бывает северная (движемся от экватора к Антарктиде) и южная (движемся от экватора к Арктике). Широта – величина угловая, измеряется в градусах.
2. Долгота – изменение положения предмета в направлении от нулевого меридиана в сторону Азии (восточная долгота) или Америки (западная долгота). Измеряется, как и широта, в градусах.
3. Высота или глубина – изменение положения предмета вверх или вниз (в глубину) от поверхности мирового океана. Измеряется в метрах с отрицательным или положительным значением. Отрицательное значение говорит о том, что объект находится на глубине, ниже уровня мирового океана.

…А нашелся я очень просто: сообщил о своих координатах в лагерь геологической экспедиции. Координаты я определил по топографической карте (они записываются на полях), согласно двух ориентиров – озера и поселения, к которым я поочередно вышел.

Общая информация об Алматы

Общая информация о городе Алматы

Почти 150 лет прошло с момента основания первого поселения на территории Алматы. За эти десятилетия, много как радостных, так и грустных страниц было перелистано в Книге судьбы города, в жизнях его обитателей. Произошло немало политических, социальных, и экономических перемен. Но обязанность каждого гражданина Казахстана с уважением относиться к своему наследию своих предков, восстанавливать портрет города на историческом фоне, передавать памятные страницы истории в событиях и лицах своим последующим поколениям.

Город Алматы расположен в центре евразийского континента, на юго-востоке Республики Казахстан. Географические координаты: 77 градусов восточной долготы и 43 градуса северной широты. Алматы находится на одной параллели с такими известными городами как Гагры и Владивосток.

Алматы живописно раскинулся в предгорьях Заилийского Алатау – самого северного горного хребта Тянь-Шаня. Так что, Алматы такой же горный город как Душанбе или Ереван. Общая площадь города – более чем 170 квадратных километров. Он расположен в долине рек Большая и Малая Алматинка и их притоков, стекающих с ледников Заилийского Алатау и горных ущелий. Горные реки и озера – главный источник водоснабжения Алматы. В горных ущельях скрыто множество водопадов и горячих радоновых и серных источников. Вокруг источников создано немало бальнеологических курортов.

В горных предместьях Алматы были построены: научная станция для изучения Солнца и космических лучей, астрофизические обсерватории на Каменском Плато и перевале Ассы, спортивные комплексы на ледовом стадионе Медео, горнолыжная станция Чимбулак, альпинистские и туристические лагеря, курорты, дома отдыха и кемпинги.

Талгар (5017 м), Комсомольский (теперь Нурсултан 4376 м) и Большой Алматинский (3684 м) – все эти пики преобладают в панораме живописных вершин, окружающих город с юга. Некоторые вершины, возвышающиеся над облаками, столь же высоки как европейский Монблан, Кавказский Казбек, и американский Таджумулько.

Климат в городе резко-континентальный со значительными колебаниями в температуре не только между сезонами, но и между временами суток. Северная сторона города близка к степям и полупустыням, близ горячего Kaskelen Moyunkuins. В южных областях, на высоте 1520-1750 метров над уровнем моря, в районе тракта Медео и Каменского плато, напротив, чувствуется дыхание ледяных «Арктических гор».

Средняя скорость ветра здесь в два раза меньше чем в Москве. Средняя июльская температура равна той, что царит на островах Шри-Ланка (Цейлон), Калимантан (Борнео) и Ява. Средняя январская температура почти такая же, как на севере Норвегии.

Солнечных дней в Алматы много: до 1596 часов в год. Также в году насчитывается до 151 дней без заморозков. Уровень температурного колебания воздуха варьируется на различных высотах: при подъеме на более чем 1400 метров выше уровня моря средняя ежегодная температура воздуха понижается на 0.66 ° каждые 100 метров . Эти и другие благоприятные климатические факторы обеспечивают уникальные возможности развития спорта и туризма в регионе.

Каньон реки Темирлик

Капал-Арасан

Большое Алматинское озеро

Богато и разнообразно царство животных и растений Заилийского Алатау. Окрестности Алматы – часть Национального парка Или-Алатау. На его территории созданы заповедники дикой природы – среда обитания многих редких птиц и животных, занесенных в Красную Книгу Казахстана. Среди них такие виды как снежный барс, изображение которого, кстати, украшает эмблему города Алматы.

У подножия гор растут зерновые и бахчевые культуры, плантации табака и виноградники сменяют фруктовые сады. Именно здесь был впервые выращен знаменитый алматинский сорт яблок «апорт». И в какой-то момент яблоко не только стало символом города, но и дало ему название («алма» – по-казахски «яблоко»).

Выше в предгорьях растут дикие яблоки, боярышник и абрикосы. Посреди горных склонов лиственные деревья и кустарники сменяют красивые Тянь-Шанские ели. Еще выше горы покрыты субальпийскими и альпийскими лугами. Эти роскошные летние пастбища («джайлау») постепенно превращаются в горную тундру и, наконец, в царство вечных ледников.

Сады, парки, общественные места и бульвары занимают более чем 8 гектаров городской территории. Среди зеленых насаждений можно увидеть экзотические растения, привезенные из Северной Америки, Крыма, Кавказа, Сибири и Дальнего Востока. Окрестности Алматы славятся такими редкими представителями местной флоры как юнона, анемон, боярышник. Забытые имена наших соотечественников, деятелей советской науки теперь воплощены в названиях многих растений: яблоня Недзветского, лук Фетизова, ель Шренка, шафран Королькова и т.д. Много имен почетных граждан были сохранены в названиях гор и долин Заилийского Алатау: ледники Палгова, Брызгалова, Дмитриева, Пояркова, Шнитникова и Войцеховского, долины Рыскулова, Колокольникова, Зимина, вершина Кудерина. Впрочем, в настоящее время большинство старых названий сменили новые.

В начале XX писатель П. Краснов писал: «в своих остроумных историях, Тэффи не без юмора отмечала, что каждый город известен чем-то своим. Дрезден знаменит своей Мадонной, Нью-Йорк – статуей Свободы, а Верный … яблоками и землетрясениями». Город также известен живописными холмами, один из которых был назван в честь выдающегося горожанина Веригина.

Один из проектов архитектора А.П. Соколова-Земана, который, к сожалению, остался неосуществленным, предусматривал строительство общественных зданий на склонах известного Веригинского холма (теперь Коктюбе), вершину которого венчал бы монументальный Дом Верховного Совета Республики. В конечном итоге, Дворец Республики был построен на бульваре Абая, а на вершине холма возведена мощная телерадиостанция с 372-метровой телевизионной башней. Полная высота структуры (вместе с холмом) составляет 1402 метра над уровнем моря.

Горы – любимое место отдыха жителей Алматы. Зимой их влекут санные и лыжные маршруты, а летом – зеленые цветущие лужайки. До вершины Коктюбе легко добраться по канатной дороге. Отсюда, с этого живописного места, обеспечивающего полную панораму «Южной столицы», можно с интересом понаблюдать за жизнью большого города. Затем зайти в одно их маленьких кафе и отведать восхитительные, аппетитные блюда казахской национальной кухни. С вершины Коктюбе, также можно продолжить экскурсию на соседние горы и долины.

Живописная природа этого края: удивительные горы, утопающие в сладко пахнущих травах, красных и синеватых маках, подснежниках, темно-красных пионах, издавна вдохновляли местных художников на создание маленьких шедевров. Алматинцам хорошо известны такие работы как «На вершине» Николая Клудова (1886 год), «Панорама Малой станицы» Абулхана Кастеева (1937год), «Долина Алатау» Обакира Исмайлова (1942 год), «Очередь на фуникулер» Евгения Содоркина (1970 год), «Новая телевизионная башня» Дмитрия Калачева (1982 год).

Замечательный пейзаж Веригинского холма и его окрестностей запечатлен в первых фильмах об Алматы: «Наш дорогой доктор» (1957 год) режиссера Ш. Эйманова, «Добро пожаловать в Алма-Ату» (1975 год) A. Нагманова, «Горы и город» (1976 год) Я. Сика, «Огни вечерней Алма-Аты», «Город яблоневого рассвета», «Алма-Ата» (1978-1981 г.г.) В. Татенко.

Именно здесь, очарованный видом Заилийского Алатау и миражами Яблоневой долины композитор Б. Ерзакович в соавторстве с поэтами Д. Абилевым и A. Лукашенко написал в 1948 году замечательные песни «Алма-Ата» и «Мой город». Именно здесь Асет Беизенов создал свой первый вальс «Ахналы Алматым». О своих чувствах к родному краю рассказывают поэты Дмитрий Снегин в поэме «Мой город» (1939 год) и Таир Жароков в поэме «Поток» (1937 год).

Уникальные природные и климатические условия Алматы повлияли на смелые научные идеи и проекты столетия. Здесь были осуществлены идеи ученого В.Н. Бучмана относительно использования солнечной энергии. Солнечный отражатель, который он изобрел и представил на выставке, в честь 15-летия Казахской ССР, на глазах изумленной публики вскипятил воду, чем привел в действие маленькую паровую машину. Кстати, благотворный эффект солнечного отражателя Бучмана был испытан в 1959 году пациентами самой первой в Республике гелиологической клиники.

Еще одна научная сенсация, произошедшая в Алматы – открытие академиком Тиховым астроботаники, определенной научной тенденции, изучающей спектрофотометрические свойства поверхности Марса и земной растительности. Многие поэты тогда в шутку утверждали, что «на Марсе будет цвести алматинский апорт».

В 1906 году в Верном вышла в свет книга утопического мыслителя Н.Ф. Федорова под названием «Философия общих причин». Книга была подготовлена к публикации учеником Федорова – адвокатом Н.П. Петерсоном. Эта работа представителя российского космизма Николая Федорова была признана всем международным сообществом как выдающийся памятник философской мысли. Философ предсказал, что придет время безнравственности и утилитарного подхода к незабвенным местам человеческой цивилизации. Кое-что подобное, к сожалению, случилось в Алматы, когда прошлое не в состоянии было сосуществовать в гармонии с настоящим, когда многие памятники и исторические места были безвозвратно утеряны…

Частые землетрясения в Верном привели к подробному изучению этого стихийного бедствия, особенностей тектоники этой местности. Вследствие чего стали разрабатываться новые методы сейсмоустойчивости Казахстана. В истории Казахстана известны две крупные геологических катастрофы: 28 мая 1887 года и 22 декабря 1910 года, а также разрушительный селевый поток, который накрыл город ночью с 8 на 9 июля 1921 года. Эти события значительно повлияли на развитие городского архитектурного планирования «Южной столицы». Чтобы защитить город от селевых потоков и наводнений, на реках Большая и Малая Алматинка и их притоках в 1973 году были установлены защитные укрепления.

Тема 3. ОСНОВНЫЕ СИСТЕМЫ КООРДИНАТ, ПРИМЕНЯЕМЫЕ В ГЕОДЕЗИИ

3.1. ГЕОДЕЗИЧЕСКАЯ СИСТЕМА КООРДИНАТ

Рис. 3.1. Геодезическая система координат

Счет геодезических широт ведется от 0 до 90° к северу и к югу от экватора. Геодезические широты Северного полушария называются северными и имеют знак « + », а Южного — южными и имеют знак «—». Геодезическая широта измеряется центральным углом в плоскости меридиана.
Геодезическая широта (в градусах) показывает, насколько данная точка на земном эллипсоиде расположена севернее или южнее плоскости экватора.
Геодезическая широта для точек, расположенных на экваторе, будет равна 0°, а для точек, расположенных на полюсах ± 90°.
Геодезической долготой (L) называется двугранный угол, заключенный между плоскостью начального меридиана и плоскостью геодезического меридиана, проходящего через данную точку.
В старину в отдельных государствах за начальный меридиан принимали меридиан, проходящий через свою главную обсерваторию. В настоящее время в Украине и в большинстве стран мира для единообразия в определении долгот условились начальным считать Гринвичский меридиан, проходящий через астрономическую обсерваторию в Гринвиче (близ Лондона). От этого меридиана ведется счет так называемого международного гринвичского времени.
Геодезическая долгота измеряется либо центральным углом в плоскости экватора или параллели, либо дугой экватора от начального (Гринвичского) меридиана до меридиана, проходящего через данную точку (М), в пределах от 0 до 180° к востоку или к западу. Геодезические долготы для точек, расположенных к востоку от меридиана Гринвича до 180°, называются восточными и считаются положительными, а к западу – западными и считаются отрицательными.
Восточная долгота обозначается буквами (в.д.) или знаком « + », западная долгота — буквами (з.д.) или знаком « – ».
Геодезическая система координат, отнесенная к эллипсоиду Красовского, была разработана в 1942 – 1943 годах, поэтому она получила название системы координат 1942 года. Вместе с ней была принята Балтийская система высот, по которой ведется отсчет абсолютных высот относительно нуля Кронштадтского футштока (Футшток — специальная рейка с делениями).

3.2. АСТРОНОМИЧЕСКАЯ СИСТЕМА КООРДИНАТ

Астрономические координаты определяют положение точки на поверхности геоида. Их можно получить путем астрономических измерений с помощью геодезических инструментов или путем математической обработки результатов геодезических измерений.
Астрономической широтой (φ) называется угол, заключенный между плоскостью земного экватора и направлением отвесной линии в данной точке.
Астрономическая широта измеряется от 0 до 90° к северу и к югу от экватора. В Северном полушарии астрономические широты называются северными, а в Южном — южными.
Отвесная линия в общем случае не совпадает с направлением нормали к поверхности земного эллипсоида. Поскольку различные по плотности массы в теле Земли распределены неравномерно, то отклонение отвесной линии (силы тяжести) от нормали различное в разных точках Земли. Так, например, в районе Кавказа отклонения отвесных линий от нормалей достигают 35″, а разность отклонений отвесных линий на противоположных берегах озера Байкал достигает 40″. В среднем величина отклонений равна 4 – 5″ (рис. 3.2).

Рис. 3.2. Астрономическая система координат

Астрономической долготой (λ) называется двугранный угол, заключенный между плоскостью начального астрономического меридиана и плоскостью астрономического меридиана, проходящего через данную точку.
Поскольку плоскость астрономического меридиана проходит через отвесную линию в данной точке на поверхности Земли, а плоскость геодезического меридиана проходит через нормаль к поверхности эллипсоида, следовательно, плоскости астрономического и геодезического меридианов не совпадают. В результате этого геодезическая широта, долгота и геодезический азимут в данной точке отличаются от астрономической широты, долготы, и астрономического (истинного) азимута. Эти расхождения будут увеличиваться там, где наблюдаются большие отклонения отвесной линии от нормали, а также в тех точках геоида, где его поверхность дальше удалена от поверхности эллипсоида.
Геодезическая и астрономическая системы координат различаются как две отдельные системы при определении местоположения объектов с точностью до 1″ (в линейной величине до 20 – 30 м). Зная астрономические координаты, можно вычислить геодезические координаты путем ввода поправок на уклонение отвесных линий от нормалей, определяемых астрономо-геодезическим методом или по специальным гравиметрическим картам.

3.3. СФЕРИЧЕСКАЯ СИСТЕМА КООРДИНАТ

При решении ряда геодезических задач и составлении карт мелких масштабов Землю принимают за сферу. Положение точек местности на сфере определяется сферическими координатами: сферической широтой и сферической долготой.
Сферическими координатами называются угловые величины (широта и долгота), определяющие положение точек местности на поверхности земной сферы относительно плоскости экватора и начального меридиана (рис. 3.2).
Сферической широтой (φ) называется угол, заключенный между плоскостью экватора и направлением из центра земной сферы на данную точку. Сферическая широта измеряется центральным углом или дугой меридиана в тех же пределах, что и геодезическая широта – от 0 до 90° к северу и к югу от экватора. Сферические широты в Северном полушарии называются северными и обозначаются знаком «+», а в Южном – южными и обозначаются знаком «–».
Сферической долготой (λ) называется двугранный угол, заключенный между плоскостью начального меридиана и плоскостью меридиана, проходящего через данную точку.
Сферическая долгота измеряется либо центральным углом в плоскости экватора или в плоскости параллели, либо дугой экватора или дугой параллели от началь­ного (Гринвичского) меридиана до меридиана, проходящего через данную точку в пределах от 0 до 180° к востоку и к западу.

Рис. 3.3. Сферическая система координат

Сферические долготы для точек, расположенных к востоку от Гринвичского меридиана до 180°, называются восточными и считаются положительными, а к западу — западными и считаются отрицательными. При решении некоторых практических задач сферическая долгота отсчитывается от 0 до 360° только к востоку от Гринвичского меридиана.
Все вычисления, связанные с автоматизированным определением координат, углов и расстояний, решаются на поверхности земной сферы с использованием формул сферической тригонометрии, поэтому поверхность земного эллипсоида проектируется на поверхность сферы.
В практике часто пользуются сферой радиусом R = 6371 км, поверхность которой равна поверхности эллипсоида. При этом максимальные погрешности в определении расстояний достигают 0,5% и углов не более 0,4°.
Длина дуги большого круга на сфере в 1секунду, равная 1852 м, называется морской милей.
Вышеназванные погрешности не позволяют реализовать точность современных средств автоматизированного определения координат. Поэтому в современных вычислителях с ЦВМ применяется формулы с учетом сжатия Земли. При этом максимальные искажения расстояний составляют 0,08% – 0,17%, а искажения углов практически отсутствуют.

3.4. ПОЛЯРНАЯ И БИПОЛЯРНАЯ СИСТЕМЫ КООРДИНАТ

Полярными координатами называются угловая и линейная величины, определяющие положение точки на плоскости относительно начала координат, принимаемого за полюс, и полярной оси. Местоположение любой точки определяется углом положения, отсчитанным от полярной оси до направления на определяемую точку, и расстоянием от полюса до этой точки (рис. 3.4).

Рис. 3.4. Полярная система координат

За полярную ось могут быть приняты: истинный или магнитный меридиан, вертикальная линия сетки и направление на любой ориентир.
При работе на местности за полярную ось принимают северное направление магнитного меридиана или направление на какой-нибудь ориентир с точки стояния.

Биполярными координатами называются две угловые или две линейные величины, определяющие местоположение точки на плоскости относительно двух исходных точек (полюсов). Положение любой точки на карте или на местности определяется двумя координатами. Этими координатами могут быть два угла положения либо два расстояния от полюсов до определяемой точки (рис. 3.5, 3.6).

Рис. 3.5. Определение места точки по двум дирекционным углам

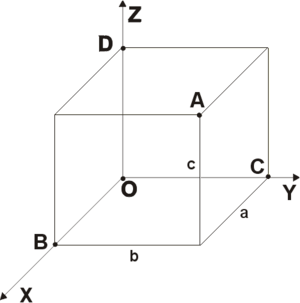
3.5. СИСТЕМА ПЛОСКИХ ПРЯМОУГОЛЬНЫХ КООРДИНАТ

Плоскими прямоугольными геодезическими координатами (прямоугольными координатами) называются линейные величины — абсцисса и ордината,— определяющие положение точки на плоскости относительно исходных направлений.

Рис. 3.7. Система плоских прямоугольных координат

Исходными направлениями служат две взаимно перпендикулярные линии (рис. 3.7) с началом отсчета в точке их пересечения (О). Прямая XX является осью абсцисс, а прямая УУ, перпендикулярная к оси абсцисс, — осью ординат. В такой системе положение любой точки на плоскости определяется кратчайшим расстоянием до нее от осей координат. Так, положение точки А определяется длиной перпендикуляров ха и уа. Отрезок ха называется абсциссой точки А, а уа — ординатой. Выражаются абсциссы и ординаты в линейной мере (обычно в метрах).
В геодезии и топографии принята правая система прямоугольных координат: это отличает ее от левой системы координат, используемой в математике. Четверти системы координат (название которых определяется принятыми обозначениями стран света), нумеруются по ходу часовой стрелки. В такой системе упрощается измерение углов ориентирования.
Абсциссы точек, расположенных вверх от начала координат, считаются положительными, а вниз от нее — отрицательными.
Ординаты точек, расположенных вправо от начала координат, считаются положительными, а влево от нее — отрицательными (см. табл. 1.2).

Четверти

Координаты

Северо-восток (СВ)
Юго-восток (ЮВ)
Юго-запад (ЮЗ)
Северо-запад (СЗ)

Система плоских прямоугольных координат применяется на ограниченных участках земной поверхности, которые могут быть приняты за плоские.
Для небольших участков начало отсчета координат может быть в любой точке участка (система с условным началом координат). В государственной системе координат за ось ординат принимают линию экватора, за ось абсцисс — направление меридиана, который называется осевым (он совпадает с направлением одной из осей системы прямоугольных координат). При проведении работ на значительных по площади территориях осевыми выбирают несколько меридианов.

3.6. ОПРЕДЕЛЕНИЕ ГЕОДЕЗИЧЕСКИХ КООРДИНАТ ТОЧЕК ПО КАРТЕ

Топографические карты печатаются отдельными листами, размеры которых установлены для каждого масштаба. Боковыми рамками листов служат меридианы, а верхней и нижней рамками – параллели. (рис. 3.9). Следовательно, географические координаты можно определить по боковым рамкам топографической карты. На всех картах верхняя рамка всегда обращена на север.
Географическую широту и долготу подписывают в углах каждого листа карты. На картах Западного полушария в северо-западном углу рамки каждого листа правее значения долготы меридиана помещают надпись: «К западу от Гринвича».
На картах масштабов 1 : 25 000 – 1 : 200 000 стороны рамок разделены на отрезки, равные 1′ (одной минуте, рис. 3.8). Эти отрезки оттенены через один и разделены точками (кроме карты масштаба 1 : 200 000) на части по 10″ (десять секунд). На каждом листе карты масштабов 1 : 50 000 и 1 : 100 000 показывают, кроме того, пересечение среднего меридиана и средней параллели с оцифровкой в градусах и минутах, а по внутренней рамке – выходы минутных делений штрихами длиной 2 – 3 мм. Это позволяет при необходимости прочерчивать параллели и меридианы на карте, склеенной из нескольких листов.

Рис. 3.8. Боковые рамки карты

При составлении карт масштабов 1 : 500 000 и 1 : 1 000 000 на них наносят картографическую сетку параллелей и меридианов. Параллели проводят соответственно через 20′ и 40′ (минут), а меридианы – через 30′ и 1°.
Географические координаты точки определяют от ближайшей параллели и от ближайшего меридиана, широта и долгота которых известны. Например, для карты масштаба 1 : 50 000 «ЗАГОРЯНИ» ближайшими параллелями будут параллели с широтами 54º40′ и 54º50′, а ближайшими меридианами будут меридиан с долготами 18º00′ и 18º15′ (рис. 3.10).

Рис. 3.9. Определение географических координат

Для определения широты заданной точки необходимо:

• одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайшую параллель (для нашей карты 54º40′);
• не меняя раствор циркуля-измерителя установить его на боковую рамку с минутными и секундными делениями, одна ножка должна быть на южной параллели (для нашей карты 54º40′), а другая – между 10-секундными точками на рамке;
• посчитать количество минут и секунд от южной параллели до второй ножки циркуля-измерителя;
• добавить полученный результат к южной широте (для нашей карты 54º40′).

Для определения долготы заданной точки необходимо:

• одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайший меридиан (для нашей карты 18º00′);
• не меняя раствор циркуля-измерителя установить его на ближайшую горизонтальную рамку с минутными и секундными делениями (для нашей карты нижнюю рамку), одна ножка должна быть на ближайшем меридиане (для нашей карты 18º00′), а другая – между 10-секундными точками на горизонтальной рамке;
• посчитать количество минут и секунд от западного (левого) меридиана до второй ножки циркуля-измерителя;
• добавить полученный результат к долготе западного меридиана (для нашей карты 18º00′).

Обратите внимание на то, что данный способ определения долготы заданной точки для карт масштаба 1:50 000 и мельче имеет погрешность за счет схождения меридианов, ограничивающих топографическую карту с востока и запада. Северная сторона рамки будет короче, чем южная. Следовательно, расхождения между измерениями долготы на северной и южной рамке могут отличаться на несколько секунд. Чтобы добиться высокой точности в результатах измерений необходимо определить долготу и по южной и по северной стороне рамки, а затем произвести интерполяцию.
Для повышения точности определения географических координат можно использовать графический метод. Для этого необходимо соединить прямыми линиями ближайшие к точке одноименные десятисекундные деления по широте к югу от точки и по долготе к западу от нее. Затем определить размеры отрезков по широте и долготе от прочерченных линий до положения точки и суммировать их соответственно с широтой и долготой прочерченных линий.
Точность определения географических координат по картам масштабов 1 : 25 000 – 1 : 200 000 составляет 2′′ и 10′′ соответственно.

Вопросы и задания для самоконтроля

1. Какие плоскости в системе географических координат являются исходными?
2. Дайте определения «геодезические координаты», «геодезическая широта», «геодезическая долгота».
3. В каких пределах измеряется геодезическая широта и геодезическая долгота?
4. Чему равна геодезическая широта точек, расположенных на экваторе и на южном полюсе?
5. Дайте определения «астрономические координаты», «астрономическая широта», «астрономическая долгота».
6. Дайте определения «сферические координаты», «сферическая широта», «сферическая долгота».
7. Чем обусловлена морская миля и какова ее длина?
8. Какие координаты называют полярными?
9. Какими величинами определяют положение точки в полярной системе координат?
10. Какими величинами определяют положение точки в биполярной системе координат?
11. Какими величинами определяют положение точки в плоской прямоугольной системе координат?
12. Какие знаки имеют плоские прямоугольные координаты х и у в I, II, III и IV четвертях?

Определение широты и долготы

При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей. Существует несколько сподручных способов это сделать. Но сначала немного теории:

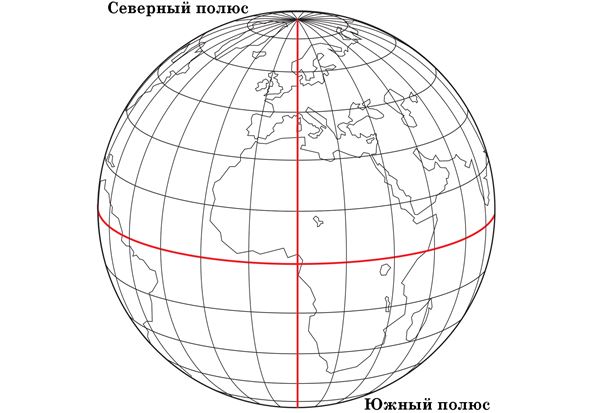
Экватор делит земной шар на северное и южное полушарие. Также существуют паралелли и меридианы. Параллели – это окружности, параллельные экватору. Меридианы- окружности, перпендикулярные экватору. Нулевой меридиан проходит через Гринвическую обсерваторию в лондоне. Система паралеллей и меридианов представляет собой координатную сетку, которая используется для определения местоположения и целеуказания.

Географические координаты состоят из широты и долготы, которые представляют собой угловые величины, с помощью которых можно определить положениеточки в любой части земного шара.

Географическая долгота – угол, отсчитываемый от нулевого меридиана, от 0° до 180°. Если счет ведется на запад от Гринвича, то это будет западной долготой, если на восток, то восточной. Долгота показывает, насколько точка находиться западнее или восточнее от нулевого меридиана.

Географическая широта, показывает насколько точка находится севернее или южнее от экватора, и составляет угол от 0° до 90°,отсчитываемый от плоскости экватора до одного из полюсов – северного или южного. Отсюда следует, что широта также бывает северной и южной.

Географические координаты измеряются в градусах, минутах и секундах. Градусом географической широты является 1/180 часть меридиана. Средняя длина одного градуса широты соответствует примерно 111,12 км. Средняя длина одной минуты соответствует 1852 м (10 кабельтовых, или 1 морской мили). Диаметр Земли (длина земной оси) между полюсами равна 12713 км.

Определение географической долготы
Градусом географической долготы является 1/360 часть экватора. Поскольку Земной шар совершает полный оборот по своей оси за 24 ч, то за 1 ч времени Земля проходит 15° долготы. Соответственно:

1° долготы = 4 мин. времени
1´ = 4 сек времени
1″ = 1/15 сек времени

Исходя из выше сказанного существует способ определения географической долготы вашего местоположения при помощи часов. Для этого необходимо иметь часы, время которых выставлено по месту с известной долготой и засечь их показания в местный полдень, а разницу этого времени перевести в градусную меру:

14:39 – 12ч = 2:39 = 39° западной долготы

Пример: Дата 7 октября. Вы определили солнечный полдень, т.е 12ч. Ваши часы выставлены по Гринвичу и показывают 8:20. Истинное солнечное время необходимо перевести в среднее, поскольку часы по Гринвичу показывают тоже среднее. Значит поправка на 7 октября составляет -12мин. (таблицы 2)

12ч – 12мин= 11:48 – среднее местное время11:48 – 8:20 = 3:28 = 55° восточной долготы, поскольку местный полдень наступил раньше Гринвического

На самом деле таблицы 1 и 2 отличаются только знаками. Например 14 мая из таблицы 1 поправка будет +3мин, а из второй -3мин. Поэтому можно пользоваться, например, таблицей 1 и приводить среднее время к истинному солнечному, а если приводить истинное солнечное к среднему, то брать противоположный знак поправки. На мой взгляд удобней приводить по первому способу, тогда вы всегда будете вносить поправку в среднее время по Гринвичу и высчитывать разницу от 12ч (истинный полдень)

Или еще проще – сначала высчитывать разницу между истинным солнечным и средним Гринвическим временем, а в полученный результат вносить поправку с учетом знака из таблицы 2.

Запомните, если в момент местного полудня время по Гринвичу будет меньше 12 часов, то у вас восточная долгота,если больше 12 часов дня, то западная. Данный метод позволяет определять долготу с точностью до 2-3°, причем находясь в экстремальных ситуациях, у вас скорее всего не окажется под рукой таблицы уравнения времени для внесения поправки на время года, поэтому только за счет этого результат будет отличаться от истинного на 0°- 4°, в зависимости от времени года.

Определение географической широты
Широту можно определить несколькими способами.

Способ №1. При помощи транспортира и отвеса. Транспортир можно смастерить из двух прямоугольных планок, скрепленных в виде циркуля, чтобы можно было менять угол между ними.

1). В центре транспортира закрепить нить с грузом, играющей роль отвеса.
2). Основание транспортира навести на полярную звезду.
3). Из угла между основанием транспортиром и отвесом вычесть 90°. Полученный результат будет углом между полярной звездой и горизонтом. Поскольку полярная звезда имеет угловое отклонение от оси полюса мира всего на 1°, то угол между полярной звездой и горизонтом будет широтой той местности, в которой вы находитесь.

1). Засечь продолжительность дня между восходом солнца на горизонте и полным его заходом.
2). В номограмме определения широты отложить в левой части полученную продолжительность дня, а в правой части дату. Соединив полученные значения прямой, определить где она пересекается со средней частью. Это пересечение и будет широтой вашей местности.

Географические координаты Алматы (широта и долгота)

Широта́ — угол φ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.

От широты места, как и от времени года, зависит продолжительность дня.

Из-за отличия формы Земли от шара географическая широта точек несколько отличается от их геоцентрической широты, т. е. от угла между направлением на данную точку из центра Земли и плоскостью экватора.

Широту места можно определить с помощью таких астрономических инструментов как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение).

Долгота

Долгота́ — угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготы от 0° до 180° к востоку от нулевого меридиана называют восточными, к западу — западными. Восточные долготы принято считать положительными, западные — отрицательными.

Выбор нулевого меридиана произволен и зависит только от соглашения. Сейчас за нулевой меридиан принят Гринвичский меридиан, проходящий через обсерваторию в Гринвиче, на юго-востоке Лондона. В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулково и т. д.

От долготы зависит местное время.

Высота

Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота. Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.

В пределах географической оболочки применяется обычно ‘высота над уровнем моря’, отсчитываемая от уровня «сглаженной» поверхности — геоида. Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений. Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.

Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако не служит координатой

Географическая система координат

В навигации в качестве начала системы координат выбирается центр масс транспортного средства (ТС). Переход начала координат из инерциальной системы координат в географическую (т.е из в ) осуществляется исходя из значений широты и долготы. Координаты центра географической системы координат в инерциальной принимают значения (при расчёте по шарообразной модели Земли):

где R — радиус земли , U — угловая скорость вращения Земли, h — высота над уровнем моря.

Ориентация осей в географической системе координат (ГСК) выбирается по алгоритму.

Ось X (другое обозначение — ось E) — ось, направленная на восток. Ось Y (другое обозначение — ось N) — ось, направленная на север. Ось Z (другое обозначение — ось Up) — ось, направленная на вертикально вверх.

Ориентация трёхгранника XYZ,из-за вращения земли и движения ТС постоянно смещается с угловыми скоростями [2] .

Основным недостатком в практическом применении ГСК в навигации является большие величины угловой скорости этой системы в высоких широтах, возрастающие вплоть до бесконечности на полюсе. Поэтому вместо ГСК используется полусвободная в азимуте СК.

Полусвободная в азимуте система координат

Полусвободная в азимуте СК отличается от ГСК только одним уравнением, которое имеет вид:

Соответственно, система имеет тоже начальное положение, что ГСК и их ориентация также совпадает с одной лишь разницей, что её оси и отклонены от соответствующих осей ГСК на угол для которого справедливо уравнение

Преобразование между ГСК и полусвободной в азимуте СК осуществляется по формуле [2]

В реальности все расчёты ведутся именно в этой системе, а потом, для выдачи выходной информации происходит преобразование координат в ГСК.

Форматы записи географических координат

Для записи географических координат используется система WGS84.

Координаты (широта от -90° до +90°, долгота от -180° до +180°) могут записываться:

• в ° градусах в виде десятичной дроби (современный вариант)
• в ° градусах и ‘ минутах с десятичной дробью
• в ° градусах, ‘ минутах и ” секундах с десятичной дробью (исторически сложившаяся форма записи)

Разделителем десятичной дроби всегда служит точка. Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+», либо буквами: «N» — северная широта и «E» — восточная долгота. Отрицательные знаки координат представляются либо знаком «-», либо буквами: «S» — южная широта и «W» — западная долгота. Буквы могут стоять как впереди, так и сзади.

Единых правил записи координат не существует.

На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаками «-» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.

В навигаторах по умолчанию чаще показываются градусы и минуты с десятичной дробью с буквенным обозначением, например, в Navitel, в iGO. Вводить координаты можно и в соответствии с другими форматами. Формат градусы и минуты рекомендуется также при радиообмене в морском деле. [источник не указан 476 дней]

В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами) [3] . Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» —- 55.755831 , 37.617673 55°45′20.99″ с. ш. 37°37′03.62″ в. д.  /  55.755831 , 37.617673 (G) (O) (Я) :

• 55.755831°, 37.617673° —- градусы
• N55.755831°, E37.617673° —- градусы (+ доп. буквы)
• 55°45.35’N, 37°37.06’E —- градусы и минуты (+ доп. буквы)
• 55°45’20.9916″N, 37°37’3.6228″E —- градусы, минуты и секунды (+ доп. буквы)

При необходимости форматы можно пересчитать самостоятельно: 1° = 60′ минутам, 1′ минута = 60″ секундам. Также можно использовать специализированные сервисы. См. ссылки.

§ 12 Как найти географический объект по координатам

• ты научишься определять географические координаты.

Для достижения цели необходимо узнать:

• что такое географические координаты;
• как определять географические координаты.

Градусная сетка

Вспомни, как называются замкнутые линии, расположенные параллельно экватору?

Как учёные называют дуги, протянутые от одного полюса к другому?

У каждого человека бывают ситуации, когда необходимо определить свое местонахождение, найти верную дорогу.
​Как найти на Земле какой-либо пункт, как узнать его географический адрес? Ты наверняка играл в игру «Морской бой», где необходимо потопить корабль противника, назвав его точный адрес, состоящий из буквы и цифры. Зная их, ты легко находишь нужную клетку, чтобы потопить корабль. Если ты внимательно рассмотришь глобус и географическую карту, то увидишь, что они тоже покрыты клетками, которые образованы пересекающимися продольными (меридианами) и поперечными (параллелями) линиями.
​На глобусах и картах меридианы и параллели проводят через одинаковое число градусов.

Параллель – это условные линии на глобусе или карте, проведённые параллельно экватору.

Меридиан – условная линия, проведённая через полюса.

• Определи, через сколько градусов изображены параллели на карте?

• А что можно сказать о меридианах?

• Отличается ли их расположение в сравнении с параллелями?

Линии меридианов и параллелей на глобусе и географических картах, разделенные на градусы, называют градусной сеткой , с помощью которой можно определить положение любого объекта на планете.

Посмотри ещё раз на изображение земного шара. В верхней и нижней части расположены обозначения полюсов Земли: Северный полюс и Южный полюс.
​Также на глобусе и карте изображён экватор, который делит​ Землю на Северное и Южное полушария.

Если началом отсчёта параллелей в градусах является экватор и он обозначает 0°, то началом отсчёта меридианов считается Гринвичский меридиан (нулевой меридиан).

Полюс – это точки пересечения воображаемой земной оси с поверхностью Земли.

Экватор – это воображаемая линия, которая делит Землю на два равных полушария: Северное и Южное.

Географические координаты

Любая точка на земном шаре имеет свой географический адрес. Этот адрес тоже состоит из двух частей – широты и долготы. Определить их позволяет градусная сеть. Широта показывает место точки на определённой параллели, а долгота – место этой точки на конкретном меридиане. Место их пересечения и есть нужный нам адрес – это географические координаты.

Географические координаты определяют положение точки относительно экватора и нулевого меридиана.

Географические координаты определяются в градусах .

Географическая широта показывает расстояние от экватора до заданной точки, выраженное в градусах. Географическая широта бывает северной и южной. У всех точек, расположенных в северном полушарии, – северная широта (с. ш.), а в южном полушарии – южная широта (ю. ш.)

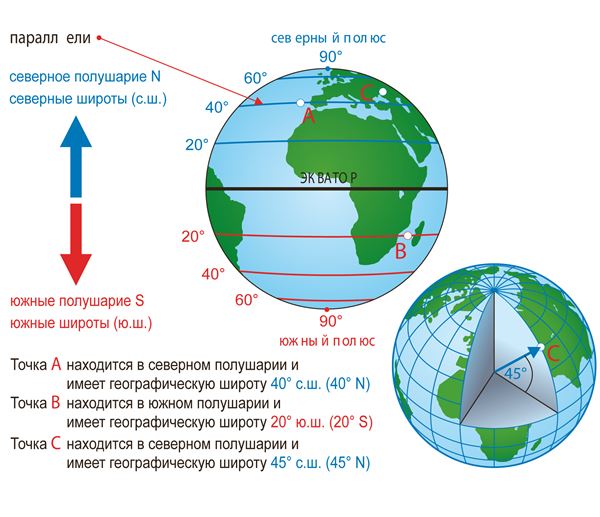
Географическая широта экватора – 0°.
​Точки, расположенные на равном расстоянии от экватора, имеют одинаковую северную и южную широту. Чем дальше от экватора находится точка, тем больше её широта.

Географическая долгота показывает расстояние от нулевого меридиана (Гринвича) до заданной точки, выраженное в градусах.
​Географическая долгота бывает западной и восточной.
​У всех точек, расположенных в западном полушарии (к западу от Гринвича), – западная долгота (з. д.), а в Восточном полушарии (к востоку от Гринвича) – восточная долгота (в. д.).
​Для определения географической долготы на карте или на глобусе изображены меридианы – линии, которые соединяют Северный и Южный полюса.

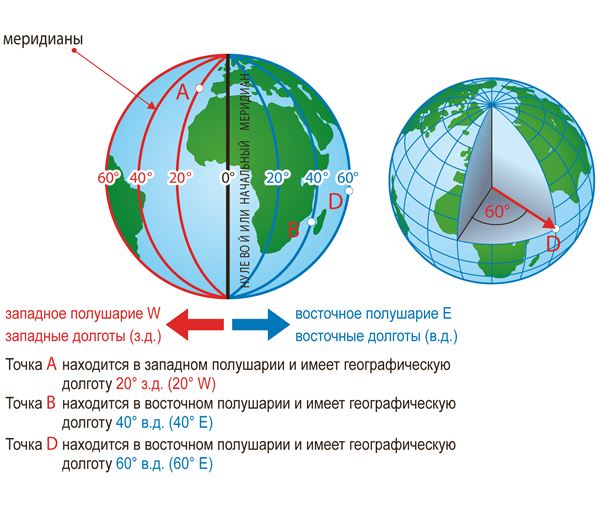
Географическая долгота начального меридиана (Гринвича) – 0°.
​Чем дальше от Гринвича находится точка, тем больше её долгота.
​Максимальное значение географической долготы – 180°, поскольку полный круг составляет 360°, то его половина (Западное полушарие или Восточное) будет равна 180°.

В какие стороны горизонта направлены

Какую форму имеет на глобусе

Каково максимальное значение в градусах?

Алгоритм определения географических координат

1. Найди географическую широту точки.

Сначала определи, в каком полушарии (в Северном или Южном) находится заданная точка. Если выше экватора, то в Северном, если ниже, то в Южном.

1. Определи, между какими параллелями (обычно они подписываются справа или слева от края карты) находится точка;
2. Выясни, сколько градусов от ближайшей со стороны экватора параллели до заданной точки.
3. В качестве примера определения географических координат используй рис. 2.

2. Определи географическую долготу точки.

1. В каком полушарии (в западном или восточном) относительно Гринвича она находится. Если слева от Гринвича, то в западном, если справа, то в восточном.
2. Определи, между какими меридианами находится точка (их долгота обычно подписывается на верхнем и на нижнем краях карты, а иногда в месте пересечения с экватором).
3. Выясни, сколько градусов до точки от ближайшего со стороны Гринвича меридиана.