Географические координаты Самары (широта и долгота)

Что такое географические координаты: широта и долгота

Определить местоположение точки на планете Земля, как и на любой другой планете сферической формы, возможно с помощью географических координат – широты и долготы. Пересечения под прямым углом кругов и дуг создают соответствующую сетку, что позволяет однозначно определить координаты. Наглядный пример – обыкновенный школьный глобус, разлинованный горизонтальными кругами и вертикальными дугами. О том, как пользоваться глобусом будет рассказано ниже.

Данная система измеряется в градусах (градус угла). Угол рассчитывается строго от центра сферы до точки на поверхности. Относительно оси, градус угла широты рассчитывается по вертикали, долготы – по горизонтали. Для вычисления точных координат существуют специальные формулы, где не редко встречается еще одна величина – высота, которая служит в основном для представления трехмерного пространства и позволяет производить вычисления для определения положения точки относительно уровня моря.

Широта и долгота – термины и определения

Земная сфера разделена воображаемой горизонтальной линией на две равные части света – северное и южное полушария – на положительный и отрицательный полюса соответственно. Так введены определения северной и южной широт. Широта представляется в виде параллельных относительно экватора кругов, называемых параллелями. Сам экватор со значением 0 градусов выступает отправной точкой для измерений. Чем ближе параллель к верхнему или нижнему полюсу, тем меньше ее диаметр и тем выше или ниже угловой градус. Например, город Москва расположен на 55-м градусе северной широты, что определяет местонахождение столицы как приблизительно равноудаленное и от экватора, и от северного полюса.

Меридиан – так называется долгота, представляемая в виде вертикальной дуги строго перпендикулярной кругам параллели. Сфера разделена на 360 меридианов. Точкой отсчета является нулевой меридиан (0 градусов), дуги которого проходят по вертикали через точки северного и южного полюсов и распространяются в восточном и западном направлениях. Таким образом определяется угол долготы от 0 до 180 градусов, вычисляемый значениями от центра до крайних точек к востоку или югу.

В отличие от широты, точкой отсчета которой служит экваториальная линия, любой меридиан может быть нулевым. Но для удобства, а именно удобства отсчета времени, определили гринвичский меридиан.

Географические координаты – место и время

Широта и долгота позволяют назначать тому или иному месту на планете точный географический адрес, измеряемый градусами. Градусы, в свою очередь, делятся на меньшие величины, такие как минуты и секунды. Каждый градус дробится на 60 частей (минут), а минута – на 60 секунд. На примере Москвы запись выглядит так: 55° 45′ 7″ N, 37° 36′ 56″ E или 55 градусов, 45 минут, 7 секунд северной широты и 37 градусов, 36 минут, 56 секунд южной долготы.

Интервал между меридианами составляет 15 градусов и около 111 км по линии экватора – такое расстояние Земля, вращаясь, проходит за один час. Для полного оборота, составляющего сутки, потребуется 24 часа.

Используем глобус

Модель Земли точно передана на глобусе с реалистичной прорисовкой всех материков, морей и океанов. В качестве вспомогательных линий проведены на карте глобуса параллели и меридианы. Практически любой глобус имеет в своей конструкции серпообразную меридиану, которая устанавливается на основании и служит вспомогательным мерилом.

Меридианная дуга оснащена специальной градусной шкалой, по которой определяется широта. Долготу можно узнать посредством еще одной шкалы – обруча, горизонтально установленного на уровне экватора. Отметив пальцем искомое место и вращая глобус вокруг своей оси к вспомогательной дуге, фиксируем значение широты (в зависимости от местонахождения объекта она окажется либо северной, либо южной). Затем отмечаем данные шкалы экватора в месте ее пересечения с меридианной дугой и определяем долготу. Узнать – восточная это или южная долгота, можно только относительно нулевого меридиана.

Определите географические координаты Владивостока (широта и долгота)

1 ответ

Владивосток расположен относительно экватора в северном полушарии, между 40 и 50 параллелями. Относительно нулевого меридиана Владивосток находится в восточном полушарии, между меридианами 130° и 140° восточной долготы.

Географические координаты Владивостока – 43° с.ш. 131° в.д.

Оценка: 4.1 ( 7 голосов)

• 1. Санкт-Петербург – географические координаты
• 2. Географические координаты города Токио
• 3. Магадан: координаты
• 4. Координаты Челябинска: широта и долгота в градусах
• 5. Географические координаты города Владивосток
• 6. Географические координаты городов России. 46 широта какие города?
• 7. Как обозначается широта и долгота?

Знаете ответ?

Предметы

Новые вопросы

Рейтинг сайта

1. 1. Алина Сайбель 468
2. 2. Лада Шадрова 220
3. 3. Игорь Проскуренко 184
4. 4. Максим Мощенков 173
5. 5. Диана Муравьёва 153
6. 6. Арина Ким 110
7. 7. Александр Кузьмин 72
8. 8. Tetiana Averkina 66
9. 9. Даниил Киселёв 54
10. 10. Марк Абрамов 46

1. 1. Кристина Волосочева 17,730
2. 2. Юлия Бронникова 17,560
3. 3. Ekaterina 17,291
4. 4. Алина Сайбель 16,670
5. 5. Darth Vader 16,611
6. 6. Мария Николаевна 15,775
7. 7. Лариса Самодурова 15,750
8. 8. Liza 15,165
9. 9. TorkMen 14,921
10. 10. Влад Лубенков 13,545

Самые активные участники недели:

• 1. Виктория Нойманн – подарочная карта книжного магазина на 500 рублей.
• 2. Bulat Sadykov – подарочная карта книжного магазина на 500 рублей.
• 3. Дарья Волкова – подарочная карта книжного магазина на 500 рублей.

Три счастливчика, которые прошли хотя бы 1 тест:

• 1. Наталья Старостина – подарочная карта книжного магазина на 500 рублей.
• 2. Николай З – подарочная карта книжного магазина на 500 рублей.
• 3. Давид Мельников – подарочная карта книжного магазина на 500 рублей.

Карты электронные(код), они будут отправлены в ближайшие дни сообщением Вконтакте или электронным письмом.

Определение широты и долготы

При попадании в аварийную ситуацию, человек первым делом должен уметь ориентироваться на местности. Иногда необходимо определить географические координаты своего местоположения, например, чтобы передать спасательной службе или для других целей. Существует несколько сподручных способов это сделать. Но сначала немного теории:

Экватор делит земной шар на северное и южное полушарие. Также существуют паралелли и меридианы. Параллели – это окружности, параллельные экватору. Меридианы- окружности, перпендикулярные экватору. Нулевой меридиан проходит через Гринвическую обсерваторию в лондоне. Система паралеллей и меридианов представляет собой координатную сетку, которая используется для определения местоположения и целеуказания.

Географические координаты состоят из широты и долготы, которые представляют собой угловые величины, с помощью которых можно определить положениеточки в любой части земного шара.

Географическая долгота – угол, отсчитываемый от нулевого меридиана, от 0° до 180°. Если счет ведется на запад от Гринвича, то это будет западной долготой, если на восток, то восточной. Долгота показывает, насколько точка находиться западнее или восточнее от нулевого меридиана.

Географическая широта, показывает насколько точка находится севернее или южнее от экватора, и составляет угол от 0° до 90°,отсчитываемый от плоскости экватора до одного из полюсов – северного или южного. Отсюда следует, что широта также бывает северной и южной.

Географические координаты измеряются в градусах, минутах и секундах. Градусом географической широты является 1/180 часть меридиана. Средняя длина одного градуса широты соответствует примерно 111,12 км. Средняя длина одной минуты соответствует 1852 м (10 кабельтовых, или 1 морской мили). Диаметр Земли (длина земной оси) между полюсами равна 12713 км.

Определение географической долготы
Градусом географической долготы является 1/360 часть экватора. Поскольку Земной шар совершает полный оборот по своей оси за 24 ч, то за 1 ч времени Земля проходит 15° долготы. Соответственно:

1° долготы = 4 мин. времени
1´ = 4 сек времени
1″ = 1/15 сек времени

Исходя из выше сказанного существует способ определения географической долготы вашего местоположения при помощи часов. Для этого необходимо иметь часы, время которых выставлено по месту с известной долготой и засечь их показания в местный полдень, а разницу этого времени перевести в градусную меру:

14:39 – 12ч = 2:39 = 39° западной долготы

Пример: Дата 7 октября. Вы определили солнечный полдень, т.е 12ч. Ваши часы выставлены по Гринвичу и показывают 8:20. Истинное солнечное время необходимо перевести в среднее, поскольку часы по Гринвичу показывают тоже среднее. Значит поправка на 7 октября составляет -12мин. (таблицы 2)

12ч – 12мин= 11:48 – среднее местное время11:48 – 8:20 = 3:28 = 55° восточной долготы, поскольку местный полдень наступил раньше Гринвического

На самом деле таблицы 1 и 2 отличаются только знаками. Например 14 мая из таблицы 1 поправка будет +3мин, а из второй -3мин. Поэтому можно пользоваться, например, таблицей 1 и приводить среднее время к истинному солнечному, а если приводить истинное солнечное к среднему, то брать противоположный знак поправки. На мой взгляд удобней приводить по первому способу, тогда вы всегда будете вносить поправку в среднее время по Гринвичу и высчитывать разницу от 12ч (истинный полдень)

Или еще проще – сначала высчитывать разницу между истинным солнечным и средним Гринвическим временем, а в полученный результат вносить поправку с учетом знака из таблицы 2.

Запомните, если в момент местного полудня время по Гринвичу будет меньше 12 часов, то у вас восточная долгота,если больше 12 часов дня, то западная. Данный метод позволяет определять долготу с точностью до 2-3°, причем находясь в экстремальных ситуациях, у вас скорее всего не окажется под рукой таблицы уравнения времени для внесения поправки на время года, поэтому только за счет этого результат будет отличаться от истинного на 0°- 4°, в зависимости от времени года.

Определение географической широты
Широту можно определить несколькими способами.

Способ №1. При помощи транспортира и отвеса. Транспортир можно смастерить из двух прямоугольных планок, скрепленных в виде циркуля, чтобы можно было менять угол между ними.

1). В центре транспортира закрепить нить с грузом, играющей роль отвеса.
2). Основание транспортира навести на полярную звезду.
3). Из угла между основанием транспортиром и отвесом вычесть 90°. Полученный результат будет углом между полярной звездой и горизонтом. Поскольку полярная звезда имеет угловое отклонение от оси полюса мира всего на 1°, то угол между полярной звездой и горизонтом будет широтой той местности, в которой вы находитесь.

1). Засечь продолжительность дня между восходом солнца на горизонте и полным его заходом.
2). В номограмме определения широты отложить в левой части полученную продолжительность дня, а в правой части дату. Соединив полученные значения прямой, определить где она пересекается со средней частью. Это пересечение и будет широтой вашей местности.

Географические координаты

Географи́ческие координа́ты — обобщённое понятие о геодезических и астрономических координатах, когда уклонение отвесной линии не учитывают [1] . Иными словами, при определении географических координат Земля принимается за шар. Географические координаты определяют положение точки на земной поверхности или, более широко, в географической оболочке. Географические координаты строятся по принципу сферических. Аналогичные координаты применяются для других планет, а также на небесной сфере [2] .

Широта́ — угол φ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.

Из-за отличия формы Земли от шара, географическая широта точек несколько отличается от их геоцентрической широты, то есть от угла между направлением на данную точку из центра Земли и плоскостью экватора.

Широту места можно определить с помощью таких астрономических инструментов, как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение).

Долгота́ — двугранный угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготу от 0° до 180° к востоку от нулевого меридиана называют восточной, к западу — западной. Восточные долготы принято считать положительными, западные — отрицательными.

Выбор нулевого меридиана произволен и зависит только от соглашения. Сейчас за нулевой меридиан принят Опорный меридиан, проходящий рядом с обсерваторией в Гринвиче, на юго-востоке Лондона. В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулкова и т. д.

Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота. Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.

В пределах географической оболочки применяется обычно высота над уровнем моря, отсчитываемая от уровня «сглаженной» поверхности — геоида. Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений. Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.

Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако ‘не’ служит координатой.

В навигации в качестве начала системы координат выбирается центр масс транспортного средства (ТС). Переход начала координат из инерциальной системы координат в географическую (то есть из O i > в O g > ) осуществляется исходя из значений широты и долготы. Координаты центра географической системы координат O g > в инерциальной принимают значения (при расчёте по шарообразной модели Земли):

X o g = ( R + h ) cos ⁡ ( φ ) cos ⁡ ( U t + λ ) =(R+h)cos(varphi )cos(Ut+lambda )> Y o g = ( R + h ) cos ⁡ ( φ ) sin ⁡ ( U t + λ ) =(R+h)cos(varphi )sin(Ut+lambda )> Z o g = ( R + h ) sin ⁡ ( φ ) =(R+h)sin(varphi )> где R — радиус земли , U — угловая скорость вращения Земли, h — высота над уровнем моря, φ — широта, λ — долгота, t — время.

Ориентация осей в географической системе координат (Г. С. К.) выбирается по схеме:

Ось X (другое обозначение — ось E) — ось, направленная на восток. Ось Y (другое обозначение — ось N) — ось, направленная на север. Ось Z (другое обозначение — ось Up) — ось, направленная вертикально вверх.

Ориентация трёхгранника XYZ,из-за вращения земли и движения Т. С. постоянно смещается с угловыми скоростями [3] .

ω E = − V N / R =-V_/R> ω N = V E / R + U cos ⁡ ( φ ) =V_/R+Ucos(varphi )> ω U p = V E R t g ( φ ) + U sin ⁡ ( φ ) =>>tg(varphi )+Usin(varphi )> где R — радиус земли , U — угловая скорость вращения Земли, V N > — скорость транспортного средства на север, V E > — на восток, φ — широта, λ — долгота.

Основным недостатком в практическом применении Г. С. К. в навигации является большие величины угловой скорости этой системы в высоких широтах, возрастающие вплоть до бесконечности на полюсе. Поэтому вместо Г. С. К. используется полусвободная в азимуте СК.

Полусвободная в азимуте система координат

Полусвободная в азимуте С. К. отличается от Г. С. К. только одним уравнением, которое имеет вид:

ω U p = U sin ⁡ ( φ ) =Usin(varphi )>

Соответственно, система имеет тоже начальное положение, осуществляется по формуле [3]

N = Y w cos ⁡ ( ε ) + X w sin ⁡ ( ε ) cos(varepsilon )+X_sin(varepsilon )> E = − Y w sin ⁡ ( ε ) + X w cos ⁡ ( ε ) sin(varepsilon )+X_cos(varepsilon )>

В реальности все расчёты ведутся именно в этой системе, а потом, для выдачи выходной информации происходит преобразование координат в ГСК.

Для записи географических координат может использоваться любой эллипсоид (или геоид), но чаще всего используются WGS 84 и Красовского (на территории РФ).

Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:

• в ° градусах в виде десятичной дроби (современный вариант)
• в ° градусах и ′ минутах с десятичной дробью
• в ° градусах, ′ минутах и ″ секундах с десятичной дробью (исторически сложившаяся форма записи)

Разделителем десятичной дроби может служить точка или запятая. Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+» либо буквами:

• «N» или «с. ш.» — северная широта,

• «E» или «в. д.» — восточная долгота.

Отрицательные знаки координат представляются либо знаком «−», либо буквами:

• «S» или «ю. ш.» — южная широта,
• «W» или «з. д.» — западная долгота.

Буквы могут стоять как впереди, так и сзади. Единых правил записи координат не существует.

На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.

В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами) [4] . Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» — 55°45′21″ с. ш. 37°37′04″ в. д. H G Я O L :

• 55,755831°, 37,617673° — градусы
• N55.755831°, E37.617673° — градусы (+ доп. буквы)
• 55°45.35′N, 37°37.06′E — градусы и минуты (+ доп. буквы)
• 55°45′20.9916″N, 37°37′3.6228″E — градусы, минуты и секунды (+ доп. буквы)

При необходимости форматы можно пересчитать самостоятельно: 1° = 60′ (минутам), 1′ (минута) = 60″ (секундам). Также можно использовать специализированные сервисы. См. ссылки.

ЕГЭ-2018 по географии: задание 1

Задание 1

(«Географические модели. Географическая карта, план местности»). 1 балл.

Тип 1. Город Дно имеет географические координаты 57°50´с.ш. 29°58´в.д. Определите, на территории какого государства находится этот город.

В этом задании необходимо найти точку на карте с предложенными координатами. Для выполнения данного задания подходит следующий алгоритм.

1. Найдём точку с координатами 0°ш. 0°д. Она расположена на пересечении экватора и нулевого (Гринвичского) меридиана в Гвинейском заливе.

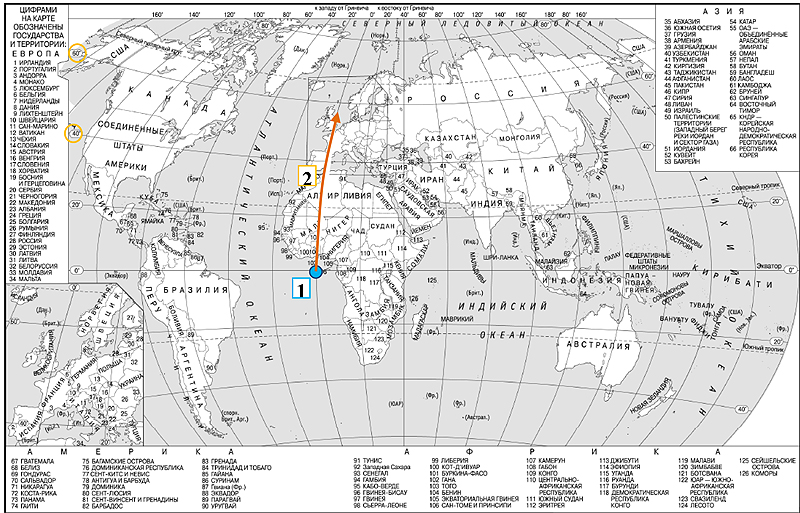
2. Первая координата искомой точки – всегда её широта, т.е. расстояние в градусах от экватора до данной точки. Чтобы его найти, нужно двигаться от точки 0°ш. 0°д. вдоль нулевого меридиана вверх (если широта искомой точки северная) или вниз (если она южная). В данном случае мы движемся на 58 градусов (57°50´ округляем для удобства*) вверх, т.к. широта северная.

Пояснение для тех, кто не понял, как мы нашли широту.

Так как значения широт (градусы параллелей) подписаны у левого и правого края карты с шагом в 20° (0°, 20°, 40°, 60° и 80°), то мы находим диапазон, в котором располагается искомая точка (40°˂58°˂60°), и мысленно разбиваем его сперва на 2 части (по 10 градусов), потом ещё на 2 части (по 5 градусов), и, наконец, на 5 частей (по градусу). В данном случае нам нужно отступить на 60° – 58° = 2° градуса от параллели 60° вниз.

3. Вторая координата искомой точки – это её долгота, т.е. расстояние в градусах от нулевого меридиана до данной точки. Чтобы его найти, нужно двигаться от найденной в п.2 точки на нулевом меридиане вправо (если долгота искомой точки восточная) или влево** (если долгота искомой точки западная) вдоль (т.е. сохраняя отступ от) ближайшей параллели. В данном случае мы перемещаемся на 30 градусов (29°58´ округляем*) вправо, т.к. долгота восточная.

Пояснение для тех, кто не понял, как мы нашли долготу.

Так как значения долгот (градусы меридианов) подписаны у верхнего и нижнего края карты с шагом в 20° (0°, 20°, 40° и т.д. до 180°), то мы находим диапазон, в котором располагается искомая точка (20°˂30°˂40°), и мысленно разбиваем его сперва на 2 части (по 10 градусов), потом ещё на 2 части (по 5 градусов), и, наконец, на 5 частей (по градусу). В данном случае нам достаточно выполнить только одно разбиение и расположить точку точно посередине между 20 и 40 меридианом.

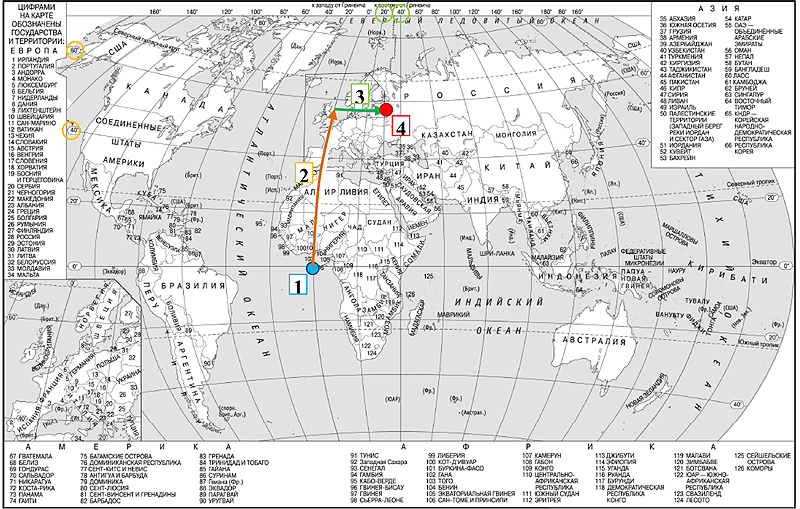
4. Определяем страну, в которой расположена искомая точка (город Дно).

Таким образом, мы выяснили, что город Дно расположен в Российской Федерации.

Алгоритм 1

(при поиске страны по карте мира):

1. Находим точку с координатами 0° ш. 0° д. (в Гвинейском заливе).
2. От неё движемся по нулевому меридиану вверх (если широта северная) или вниз (если широта южная) на указанное количество градусов.
3. От нулевого меридиана движемся вдоль параллели вправо (если долгота восточная) или влево** (если долгота западная) на указанное количество градусов.
4. Определяем, на территории какого государства расположена полученная точка, записываем его в форму ответа.

* Ремарка о правилах округления: т.к. в данном задании координаты приведены с точностью до минуты дуги, а в одном градусе 60 (а не 100) минут, то минуты до 29´ округляются в меньшую сторону (градусы остаются те же), а начиная с 30´ – в большую (к числу градусов прибавляем единицу).

** Надо отметить, что точки с координатами 140-180° западной долготы будут располагаться в правой части предложенной карты, т.к. нулевой меридиан на ней смещён влево на 40°, но мне пока ни разу не попадались города из этой области карты, поэтому я не стал усложнять алгоритм.

Тип 2. Город Мирный имеет географические координаты 62°32´ с.ш. 113°57´ в.д. Определите, на территории какого субъекта федерации находится этот город.

Отличие этого типа задания от первого заключается в том, что для его выполнения необходимо использовать не политическую карту мира, а карту административно-территориального устройства России. Сделать это задание ещё проще, т.к. все города в России имеют северную широту и восточную долготу*. Единственное, с чем здесь нужно разобраться, – это с расположением параллелей и меридианов на карте России.

Параллели на карте России изображаются в форме дуг, концентрически описанных вокруг Северного полюса. Меридианы представляют собой прямые, расходящиеся веером от Северного полюса. Иногда возникает путаница при определении градуса нужной параллели, т.к. некоторые параллели и меридианы пересекаются в районе рамки карты и их подписи расположены очень близко. Мы рекомендуем вам просто запомнить**, как проходят параллели по территории России, и при выполнении задания только проверять себя, а не искать их заново.

1. Так как территория России вытянута с запада на восток, то при выполнении этого типа задания удобнее начинать со второй координаты – долготы. Находим ближайший к городу Мирному меридиан – 110°в.д., и на нём – точку пересечения с 60 параллелью (т.к. она проходит практически посередине страны).

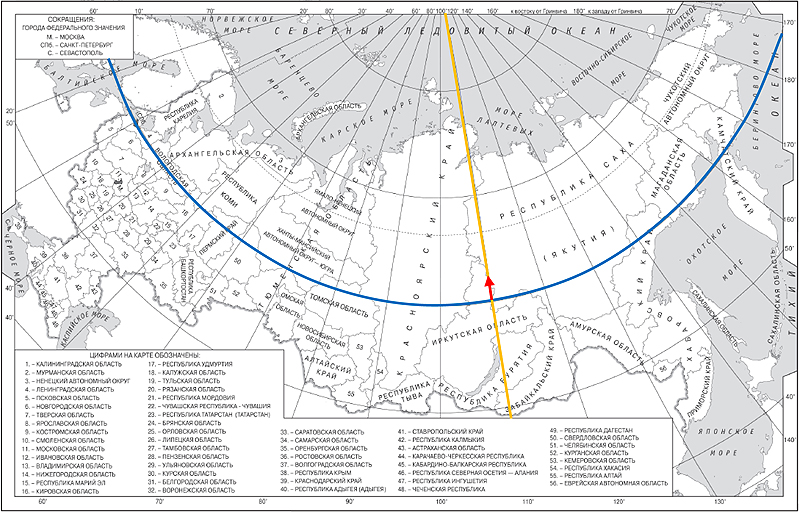
2. Теперь определим широту. От найденной в п.1 точки (60°с.ш., 110°в.д.) мы движемся вдоль меридиана по направлению к Северному полюсу (вверх) на 2°32′ (62°32′ – 60°). Это будет четверть расстояния до пересечения с 70 параллелью.

3. Уточняем долготу. От полученной в п.2 точки (62°32′ с.ш., 110 в.д.) смещаемся вдоль параллели на восток (вправо и немного вверх в данном случае) на 3°57´ (113°57´ – 110°). Это будет около 2/5 расстояния до пересечения со 120 меридианом.

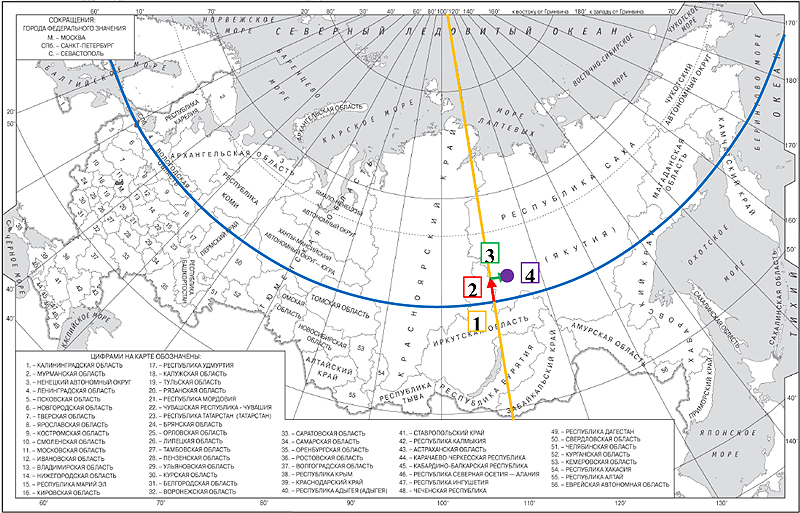
4. Определяем субъект федерации, в котором расположена искомая точка (город Мирный).

Таким образом, мы выяснили, что город Мирный расположен на территории республики Саха (Якутия).

Алгоритм 2

(при поиске субъекта федерации по карте России):

1. Находим ближайший к данному городу меридиан и точку его пересечения с 60 параллелью.
2. От неё движемся вдоль меридиана к Северному полюсу (если широта больше 60°) или от него (если широта меньше 60°) на |x-60°| градусов (x – широта города).
3. Далее движемся вдоль параллели для уточнения долготы точки.

Определяем, на территории какого субъекта федерации расположена полученная точка, записываем его в форму ответа.

* При том, что восточная часть п-ова Чукотка лежит в западном полушарии, ни одного города там не расположено.

** Так, 80-я параллель (самая маленькая дуга) проходит по архипелагам в Северном Ледовитом океане, 70-я – от северного побережья Кольского полуострова до северного побережья Чукотки, 60-я – точно через Санкт-Петербург, 50-я – вдоль южной границы Восточной Сибири, 40-ая к югу от границ России (на карте видна в районе Азербайджана и Японского моря)

Тема 3. КООРДИНАТЫ ТОЧЕК НА ЗЕМНОЙ ПОВЕРХНОСТИ

3.1. ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ

Рис. 3.1. Градусная сетка земной поверхности

Долгота – угловая величина, определяющая положение точки на Земле в направлении Запад-Восток от Гринвичского меридиана. Долготы отсчитывают от 0 до 180°, на восток – со знаком «плюс», на запад – со знаком «минус». На глобусах и картах широту показывают при помощи меридианов.

Рис. 3.3. Географическая долгота

3.1.1. Сферические координаты

Сферическими географическими координатами называют угловые величины (широта и долгота), определяющие положение точек местности на поверхности земной сферы относительно плоскости экватора и начального меридиана.

Сферической широтой (φ) называют угол между радиусом-вектором (линия, соединяющая центр сферы и заданную точку) и плоскостью экватора.

Сферическая долгота (λ) – это угол между плоскостью нулевого меридиана и плоскостью меридиана заданной точки (плоскость проходит через заданную точку и ось вращения).

Рис. 3.4. Географическая сферическая система координат

В практике топографии используют сферу радиусом R = 6371 км, поверхность которой равна поверхности эллипсоида. На такой сфере длину дуги большого круга в 1 минуту (1852 м) называют морской милей.

3.1.2. Астрономические координаты

Астрономическими географическими координатами являются широта и долгота, определяющие положение точек на поверхности геоида относительно плоскости экватора и плоскости одного из меридианов, принятого за начальный (рис. 3.5).

Астрономической широтой (φ) называется угол, образованный отвесной линией, проходящей через данную точку и плоскостью, перпендикулярной к оси вращения Земли.

Плоскость астрономического меридиана – плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
Астрономический меридиан – линия пересечения поверхности геоида с плоскостью астрономического меридиана.

Астрономической долготой (λ) называется двугранный угол между плоскостью астрономического меридиана, проходящего через данную точку, и плоскостью Гринвичского меридиана, принятого за начальный.

Рис. 3.5. Астрономическая широта (φ) и астрономическая долгота (λ)

3.1.3. Геодезическая система координат

В геодезической географической системе координат за поверхность, на которой находят положения точек, принимается поверхность референц–эллипсоида. Положение точки на поверхности референц-эллипсоида определяется двумя угловыми величинами – геодезической широтой (В) и геодезической долготой (L).
Плоскость геодезического меридиана – плоскость, проходящая через нормаль к поверхности земного эллипсоида в данной точке и параллельная его малой оси.
Геодезический меридиан – линия, по которой плоскость геодезического меридиана пересекает поверхность эллипсоида.
Геодезическая параллель – линия пересечения поверхности эллипсоида плоскостью, проходящей через данную точку и перпендикулярной к малой оси.

Геодезическая широта (В) – угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью экватора.

Геодезическая долгота (L) – двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью начального геодезического меридиана.

3.2. ОПРЕДЕЛЕНИЕ ГЕОГРАФИЧЕСКИХ КООРДИНАТ ТОЧЕК ПО КАРТЕ

Топографические карты печатаются отдельными листами, размеры которых установлены для каждого масштаба. Боковыми рамками листов служат меридианы, а верхней и нижней рамками – параллели. (рис. 3.7). Следовательно, географические координаты можно определить по боковым рамкам топографической карты. На всех картах верхняя рамка всегда обращена на север.
Географическую широту и долготу подписывают в углах каждого листа карты. На картах Западного полушария в северо-западном углу рамки каждого листа правее значения долготы меридиана помещают надпись: «К западу от Гринвича».
На картах масштабов 1 : 25 000 – 1 : 200 000 стороны рамок разделены на отрезки, равные 1′ (одной минуте, рис. 3.7). Эти отрезки оттенены через один и разделены точками (кроме карты масштаба 1 : 200 000) на части по 10″ (десять секунд). На каждом листе карты масштабов 1 : 50 000 и 1 : 100 000 показывают, кроме того, пересечение среднего меридиана и средней параллели с оцифровкой в градусах и минутах, а по внутренней рамке – выходы минутных делений штрихами длиной 2 – 3 мм. Это позволяет при необходимости прочерчивать параллели и меридианы на карте, склеенной из нескольких листов.

Рис. 3.7. Боковые рамки карты

При составлении карт масштабов 1 : 500 000 и 1 : 1 000 000 на них наносят картографическую сетку параллелей и меридианов. Параллели проводят соответственно через 20′ и 40′ (минут), а меридианы – через 30′ и 1°.
Географические координаты точки определяют от ближайшей южной параллели и от ближайшего западного меридиана, широта и долгота которых известны. Например, для карты масштаба 1 : 50 000 «ЗАГОРЯНИ» ближайшей параллелью, расположенной к югу от заданной точки, будет параллель 54º40′ с.ш., а ближайшим меридианом, расположенным западнее точки – меридиан 18º00′ в.д. (рис. 3.7).

Рис. 3.8. Определение географических координат

Для определения широты заданной точки необходимо:

• одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайшую параллель (для нашей карты 54º40′);
• не меняя раствор циркуля-измерителя, установить его на боковую рамку с минутными и секундными делениями, одна ножка должна быть на южной параллели (для нашей карты 54º40′), а другая – между 10-секундными точками на рамке;
• посчитать количество минут и секунд от южной параллели до второй ножки циркуля-измерителя;
• добавить полученный результат к южной широте (для нашей карты 54º40′).

Для определения долготы заданной точки необходимо:

• одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайший меридиан (для нашей карты 18º00′);
• не меняя раствор циркуля-измерителя, установить его на ближайшую горизонтальную рамку с минутными и секундными делениями (для нашей карты нижнюю рамку), одна ножка должна быть на ближайшем меридиане (для нашей карты 18º00′), а другая – между 10-секундными точками на горизонтальной рамке;
• посчитать количество минут и секунд от западного (левого) меридиана до второй ножки циркуля-измерителя;
• добавить полученный результат к долготе западного меридиана (для нашей карты 18º00′).

Обратите внимание на то, что данный способ определения долготы заданной точки для карт масштаба 1:50 000 и мельче имеет погрешность за счет схождения меридианов, ограничивающих топографическую карту с востока и запада. Северная сторона рамки будет короче, чем южная. Следовательно, расхождения между измерениями долготы на северной и южной рамке могут отличаться на несколько секунд. Чтобы добиться высокой точности в результатах измерений, необходимо определить долготу и по южной и по северной стороне рамки, а затем произвести интерполяцию.
Для повышения точности определения географических координат можно использовать графический метод. Для этого необходимо соединить прямыми линиями ближайшие к точке одноименные десятисекундные деления по широте к югу от точки и по долготе к западу от нее. Затем определить размеры отрезков по широте и долготе от прочерченных линий до положения точки и суммировать их соответственно с широтой и долготой прочерченных линий.
Точность определения географических координат по картам масштабов 1 : 25 000 – 1 : 200 000 составляет 2″ и 10″ соответственно.

3.3. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ

Полярными координатами называют угловую и линейную величины, определяющие положение точки на плоскости относительно начала координат, принимаемого за полюс (О), и полярной оси (ОС) (рис. 3.1).

Местоположение любой точки (М) определяется углом положения (α), отсчитанным от полярной оси до направления на определяемую точку, и расстоянием (горизонтальным проложением – проекцией линии местности на горизонтальную плоскость) от полюса до этой точки (Д). Полярные углы обычно отсчитывают от полярной оси по направлению движения часовой стрелки.

Рис. 3.9. Полярная система координат

За полярную ось могут быть приняты: истинный меридиан, магнитный меридиан, вертикальная линия сетки, направление на любой ориентир.

3.2. БИПОЛЯРНЫЕ СИСТЕМЫ КООРДИНАТ

Биполярными координатами называют две угловые или две линейные величины, определяющие местоположение точки на плоскости относительно двух исходных точек (полюсов О ₁ и О ₂ рис. 3.10).

Положение любой точки определяется двумя координатами. Этими координатами могут быть либо два угла положения (α ₁ и α ₂ рис. 3.10), либо два расстояния от полюсов до определяемой точки (Д ₁ и Д ₂ рис. 3.11).

Рис. 3.11. Определение места точки по двум расстояниям

В биполярной системе координат положение полюсов известно, т.е. известно расстояние между ними.

Ранее были рассмотрены плановые системы координат, определяющие положение любой точки на поверхности земного эллипсоида, либо референц-эллипсоида, либо на плоскости. Однако эти плановые системы координат не позволяют получить однозначное положение точки на физической поверхности Земли. Географические координаты относят положение точки к поверхности референц-эллипсоида, полярные и биполярные кординаты относят положение точки к плоскости. И все эти определения никак не касаются физической поверхности Земли, которая для географа и является более интересной, чем референц-эллипсоид.
Таким образом, плановые системы координат не дают возможности однозначно определить положение данной точки. Необходимо как-то определить своё положение хотя бы словами «выше», «ниже». Только относительно чего? Для получения полной информации о положении точки на физической поверхности Земли используется третья координата – высота. Поэтому и возникает необходимость рассмотреть третью систему координат – систему высот.

Расстояние по отвесной линии от уровенной поверхности до точки физической поверхности Земли называют высотой.

Высоты бывают абсолютные, если их отсчет ведется от уровенной поверхности Земли, и относительные (условные), если их отсчет ведется от произвольной уровенной поверхности. Обычно за начало отсчета абсолютных высот принимают уровень океана или открытого моря в спокойном состоянии. В России и Украине за начало отсчета абсолютных высот принят нуль Кронштадтского футштока.

Футшток – рейка с делениями, укрепленная отвесно на берегу так, чтобы обеспечивалась возможность определения по ней положения поверхности воды, находящейся в спокойном состоянии.
Кронштадтский футшток – черта на медной пластине (доске), вмонтированной в гранитный устой Синего моста Обводного канала в г. Кронштадте.
Первый футшток был установлен во времена правления Петра 1, и с 1703 г. начались регулярные наблюдения за уровнем Балтийского моря. Вскоре футшток был разрушен и только с 1825 г. (и до настоящего времени) были возобновлены регулярные наблюдения. В 1840 г. гидрографом М.Ф.Рейнекебыла вычислена средняя высота уровня Балтийского моря и зафиксирована на гранитном устое моста в виде глубокой горизонтальной черты. С 1872 г. эта черта принята за нулевую отметку при вычислении высот всех точек на территории Российского государства. Кронштадский футшток неоднократно видоизменялся, однако положение его основной отметки при изменениях конструкции сохраняли прежней, т.е. определенной в 1840 г.
После распада Советского Союза украинские геодезисты не стали изобретать свою национальную систему высот, и в настоящее время в Украине по-прежнему используется Балтийская система высот.

Следует отметить, что в каждом необходимом случае не ведут измерения непосредственно от уровня Балтийского моря. Существуют на местности специальные точки, высоты которых заранее были определены в Балтийской системе высот. Эти точки называют реперами.
Абсолютные высоты H могут быть положительными (для точек выше уровня Балтийского моря), и отрицательными (для точек ниже уровня Балтийского моря).
Разность абсолютных высот двух точек называют относительной высотой или превышением (h):
h =H_А −H_В .
Превышение одной точки над другой также может быть положительным и отрицательным. Если абсолютная высота точки А больше абсолютной высоты точки В, т.е. находится выше точки В, то превышение точки А над точкой В будет положительным, и наоборот, превышение точки В над точкой А – отрицательным.

Пример. Абсолютная высота точки А равна Н_А = +124,78 м. Превышение точки С над точкой А равно h_С(А) = –165,06 м. Найти абсолютную высоту точки С.

Численное значение высоты называют отметкой точки (абсолютной или условной).
Например, Н_А = 528,752 м – абсолютная отметка точки А; Н’_В = 28,752 м – условная отметка точки В .

Рис. 3.12. Высоты точек земной поверхности

Для перехода от условных высот к абсолютным и наоборот необходимо знать расстояние от основной уровенной поверхности до условной.

Вопросы и задания для самоконтроля

1. Раскройте понятия: полюс, плоскость экватора, экватор, плоскость меридиана, меридиан, параллель, градусная сетка, координаты.
2. Относительно каких плоскостей на земном шаре (эллипсоиде вращения) определяют географические координаты?
3. В чем отличие астрономических географических координат от геодезических?
4. С помощью чертежа раскройте понятия «сферическая широта» и «сферическая долгота».
5. На какой поверхности определяют положение точек в астрономической системе координат?
6. С помощью чертежа раскройте понятия «астрономическая широта» и «астрономическая долгота».
7. На какой поверхности определяют положение точек в геодезической системе координат?
8. С помощью чертежа раскройте понятия «геодезическая широта» и «геодезическая долгота».
9. Почему для повышения точности определения долготы необходимо соединить прямыми линиями ближайшие к точке одноименные десятисекундные деления?
10. Как можно рассчитать широту точки, если определить количество минут и секунд от северной рамки топографической карты?
11. Какие координаты называют полярными?
12. Для каких целей в полярной системе координат служит полярная ось?
13. Какие координаты называют биполярными?
14. В чем сущность прямой геодезической задачи?
15. В чем сущность обратной геодезической задачи?
16. Какую величину называют приращением координат?
17. Дайте определения синуса, косинуса, тангенса и котангенса угла.
18. Как можно применить в топографии теорему Пифагора о соотношении между сторонами прямоугольного треугольника?
19. Какую величину называют высотой точки?
20. Раскройте понятия: «абсолютная высота точки», «относительная высота точки».
21. Как рассчитать абсолютную высоту второй точки, если известны абсолютная высота первой точки и превышение второй точки над первой?
22. Какую уровенную поверхность принято считать началом отсчета абсолютных высот в Украине?
23. Как называют численное значение высоты?