Тема 3. КООРДИНАТЫ ТОЧЕК НА ЗЕМНОЙ ПОВЕРХНОСТИ
3.1. ГЕОГРАФИЧЕСКИЕ КООРДИНАТЫ
Рис. 3.1. Градусная сетка земной поверхности
Долгота – угловая величина, определяющая положение точки на Земле в направлении Запад-Восток от Гринвичского меридиана. Долготы отсчитывают от 0 до 180°, на восток – со знаком «плюс», на запад – со знаком «минус». На глобусах и картах широту показывают при помощи меридианов.
Рис. 3.3. Географическая долгота
3.1.1. Сферические координаты
Сферическими географическими координатами называют угловые величины (широта и долгота), определяющие положение точек местности на поверхности земной сферы относительно плоскости экватора и начального меридиана.
Сферической широтой (φ) называют угол между радиусом-вектором (линия, соединяющая центр сферы и заданную точку) и плоскостью экватора.
Сферическая долгота (λ) – это угол между плоскостью нулевого меридиана и плоскостью меридиана заданной точки (плоскость проходит через заданную точку и ось вращения).
Рис. 3.4. Географическая сферическая система координат
В практике топографии используют сферу радиусом R = 6371 км, поверхность которой равна поверхности эллипсоида. На такой сфере длину дуги большого круга в 1 минуту (1852 м) называют морской милей.
3.1.2. Астрономические координаты
Астрономическими географическими координатами являются широта и долгота, определяющие положение точек на поверхности геоида относительно плоскости экватора и плоскости одного из меридианов, принятого за начальный (рис. 3.5).
Астрономической широтой (φ) называется угол, образованный отвесной линией, проходящей через данную точку и плоскостью, перпендикулярной к оси вращения Земли.
Плоскость астрономического меридиана – плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
Астрономический меридиан – линия пересечения поверхности геоида с плоскостью астрономического меридиана.
Астрономической долготой (λ) называется двугранный угол между плоскостью астрономического меридиана, проходящего через данную точку, и плоскостью Гринвичского меридиана, принятого за начальный.
Рис. 3.5. Астрономическая широта (φ) и астрономическая долгота (λ)
3.1.3. Геодезическая система координат
В геодезической географической системе координат за поверхность, на которой находят положения точек, принимается поверхность референц–эллипсоида. Положение точки на поверхности референц-эллипсоида определяется двумя угловыми величинами – геодезической широтой (В) и геодезической долготой (L).
Плоскость геодезического меридиана – плоскость, проходящая через нормаль к поверхности земного эллипсоида в данной точке и параллельная его малой оси.
Геодезический меридиан – линия, по которой плоскость геодезического меридиана пересекает поверхность эллипсоида.
Геодезическая параллель – линия пересечения поверхности эллипсоида плоскостью, проходящей через данную точку и перпендикулярной к малой оси.
Геодезическая широта (В) – угол, образованный нормалью к поверхности земного эллипсоида в данной точке и плоскостью экватора.
Геодезическая долгота (L) – двугранный угол между плоскостью геодезического меридиана данной точки и плоскостью начального геодезического меридиана.
3.2. ОПРЕДЕЛЕНИЕ ГЕОГРАФИЧЕСКИХ КООРДИНАТ ТОЧЕК ПО КАРТЕ
Топографические карты печатаются отдельными листами, размеры которых установлены для каждого масштаба. Боковыми рамками листов служат меридианы, а верхней и нижней рамками – параллели. (рис. 3.7). Следовательно, географические координаты можно определить по боковым рамкам топографической карты. На всех картах верхняя рамка всегда обращена на север.
Географическую широту и долготу подписывают в углах каждого листа карты. На картах Западного полушария в северо-западном углу рамки каждого листа правее значения долготы меридиана помещают надпись: «К западу от Гринвича».
На картах масштабов 1 : 25 000 – 1 : 200 000 стороны рамок разделены на отрезки, равные 1′ (одной минуте, рис. 3.7). Эти отрезки оттенены через один и разделены точками (кроме карты масштаба 1 : 200 000) на части по 10″ (десять секунд). На каждом листе карты масштабов 1 : 50 000 и 1 : 100 000 показывают, кроме того, пересечение среднего меридиана и средней параллели с оцифровкой в градусах и минутах, а по внутренней рамке – выходы минутных делений штрихами длиной 2 – 3 мм. Это позволяет при необходимости прочерчивать параллели и меридианы на карте, склеенной из нескольких листов.
Рис. 3.7. Боковые рамки карты
При составлении карт масштабов 1 : 500 000 и 1 : 1 000 000 на них наносят картографическую сетку параллелей и меридианов. Параллели проводят соответственно через 20′ и 40′ (минут), а меридианы – через 30′ и 1°.
Географические координаты точки определяют от ближайшей южной параллели и от ближайшего западного меридиана, широта и долгота которых известны. Например, для карты масштаба 1 : 50 000 «ЗАГОРЯНИ» ближайшей параллелью, расположенной к югу от заданной точки, будет параллель 54º40′ с.ш., а ближайшим меридианом, расположенным западнее точки – меридиан 18º00′ в.д. (рис. 3.7).
Рис. 3.8. Определение географических координат
Для определения широты заданной точки необходимо:
- одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайшую параллель (для нашей карты 54º40′);
- не меняя раствор циркуля-измерителя, установить его на боковую рамку с минутными и секундными делениями, одна ножка должна быть на южной параллели (для нашей карты 54º40′), а другая – между 10-секундными точками на рамке;
- посчитать количество минут и секунд от южной параллели до второй ножки циркуля-измерителя;
- добавить полученный результат к южной широте (для нашей карты 54º40′).
Для определения долготы заданной точки необходимо:
- одну ножку циркуля-измерителя установить на заданную точку, другую ножку по кратчайшему расстоянию установить на ближайший меридиан (для нашей карты 18º00′);
- не меняя раствор циркуля-измерителя, установить его на ближайшую горизонтальную рамку с минутными и секундными делениями (для нашей карты нижнюю рамку), одна ножка должна быть на ближайшем меридиане (для нашей карты 18º00′), а другая – между 10-секундными точками на горизонтальной рамке;
- посчитать количество минут и секунд от западного (левого) меридиана до второй ножки циркуля-измерителя;
- добавить полученный результат к долготе западного меридиана (для нашей карты 18º00′).
Обратите внимание на то, что данный способ определения долготы заданной точки для карт масштаба 1:50 000 и мельче имеет погрешность за счет схождения меридианов, ограничивающих топографическую карту с востока и запада. Северная сторона рамки будет короче, чем южная. Следовательно, расхождения между измерениями долготы на северной и южной рамке могут отличаться на несколько секунд. Чтобы добиться высокой точности в результатах измерений, необходимо определить долготу и по южной и по северной стороне рамки, а затем произвести интерполяцию.
Для повышения точности определения географических координат можно использовать графический метод. Для этого необходимо соединить прямыми линиями ближайшие к точке одноименные десятисекундные деления по широте к югу от точки и по долготе к западу от нее. Затем определить размеры отрезков по широте и долготе от прочерченных линий до положения точки и суммировать их соответственно с широтой и долготой прочерченных линий.
Точность определения географических координат по картам масштабов 1 : 25 000 – 1 : 200 000 составляет 2″ и 10″ соответственно.
3.3. ПОЛЯРНАЯ СИСТЕМА КООРДИНАТ
Полярными координатами называют угловую и линейную величины, определяющие положение точки на плоскости относительно начала координат, принимаемого за полюс (О), и полярной оси (ОС) (рис. 3.1).
Местоположение любой точки (М) определяется углом положения (α), отсчитанным от полярной оси до направления на определяемую точку, и расстоянием (горизонтальным проложением – проекцией линии местности на горизонтальную плоскость) от полюса до этой точки (Д). Полярные углы обычно отсчитывают от полярной оси по направлению движения часовой стрелки.
Рис. 3.9. Полярная система координат
За полярную ось могут быть приняты: истинный меридиан, магнитный меридиан, вертикальная линия сетки, направление на любой ориентир.
3.2. БИПОЛЯРНЫЕ СИСТЕМЫ КООРДИНАТ
Биполярными координатами называют две угловые или две линейные величины, определяющие местоположение точки на плоскости относительно двух исходных точек (полюсов О 1 и О 2 рис. 3.10).
Положение любой точки определяется двумя координатами. Этими координатами могут быть либо два угла положения (α 1 и α 2 рис. 3.10), либо два расстояния от полюсов до определяемой точки (Д 1 и Д 2 рис. 3.11).
Рис. 3.11. Определение места точки по двум расстояниям
В биполярной системе координат положение полюсов известно, т.е. известно расстояние между ними.
Ранее были рассмотрены плановые системы координат, определяющие положение любой точки на поверхности земного эллипсоида, либо референц-эллипсоида, либо на плоскости. Однако эти плановые системы координат не позволяют получить однозначное положение точки на физической поверхности Земли. Географические координаты относят положение точки к поверхности референц-эллипсоида, полярные и биполярные кординаты относят положение точки к плоскости. И все эти определения никак не касаются физической поверхности Земли, которая для географа и является более интересной, чем референц-эллипсоид.
Таким образом, плановые системы координат не дают возможности однозначно определить положение данной точки. Необходимо как-то определить своё положение хотя бы словами «выше», «ниже». Только относительно чего? Для получения полной информации о положении точки на физической поверхности Земли используется третья координата – высота. Поэтому и возникает необходимость рассмотреть третью систему координат – систему высот.
Расстояние по отвесной линии от уровенной поверхности до точки физической поверхности Земли называют высотой.
Высоты бывают абсолютные, если их отсчет ведется от уровенной поверхности Земли, и относительные (условные), если их отсчет ведется от произвольной уровенной поверхности. Обычно за начало отсчета абсолютных высот принимают уровень океана или открытого моря в спокойном состоянии. В России и Украине за начало отсчета абсолютных высот принят нуль Кронштадтского футштока.
Футшток – рейка с делениями, укрепленная отвесно на берегу так, чтобы обеспечивалась возможность определения по ней положения поверхности воды, находящейся в спокойном состоянии.
Кронштадтский футшток – черта на медной пластине (доске), вмонтированной в гранитный устой Синего моста Обводного канала в г. Кронштадте.
Первый футшток был установлен во времена правления Петра 1, и с 1703 г. начались регулярные наблюдения за уровнем Балтийского моря. Вскоре футшток был разрушен и только с 1825 г. (и до настоящего времени) были возобновлены регулярные наблюдения. В 1840 г. гидрографом М.Ф.Рейнекебыла вычислена средняя высота уровня Балтийского моря и зафиксирована на гранитном устое моста в виде глубокой горизонтальной черты. С 1872 г. эта черта принята за нулевую отметку при вычислении высот всех точек на территории Российского государства. Кронштадский футшток неоднократно видоизменялся, однако положение его основной отметки при изменениях конструкции сохраняли прежней, т.е. определенной в 1840 г.
После распада Советского Союза украинские геодезисты не стали изобретать свою национальную систему высот, и в настоящее время в Украине по-прежнему используется Балтийская система высот.
Следует отметить, что в каждом необходимом случае не ведут измерения непосредственно от уровня Балтийского моря. Существуют на местности специальные точки, высоты которых заранее были определены в Балтийской системе высот. Эти точки называют реперами.
Абсолютные высоты H могут быть положительными (для точек выше уровня Балтийского моря), и отрицательными (для точек ниже уровня Балтийского моря).
Разность абсолютных высот двух точек называют относительной высотой или превышением (h):
h =HА −HВ .
Превышение одной точки над другой также может быть положительным и отрицательным. Если абсолютная высота точки А больше абсолютной высоты точки В, т.е. находится выше точки В, то превышение точки А над точкой В будет положительным, и наоборот, превышение точки В над точкой А – отрицательным.
Пример. Абсолютная высота точки А равна НА = +124,78 м. Превышение точки С над точкой А равно hС(А) = –165,06 м. Найти абсолютную высоту точки С.
Численное значение высоты называют отметкой точки (абсолютной или условной).
Например, НА = 528,752 м – абсолютная отметка точки А; Н’В = 28,752 м – условная отметка точки В .
Рис. 3.12. Высоты точек земной поверхности
Для перехода от условных высот к абсолютным и наоборот необходимо знать расстояние от основной уровенной поверхности до условной.
Вопросы и задания для самоконтроля
- Раскройте понятия: полюс, плоскость экватора, экватор, плоскость меридиана, меридиан, параллель, градусная сетка, координаты.
- Относительно каких плоскостей на земном шаре (эллипсоиде вращения) определяют географические координаты?
- В чем отличие астрономических географических координат от геодезических?
- С помощью чертежа раскройте понятия «сферическая широта» и «сферическая долгота».
- На какой поверхности определяют положение точек в астрономической системе координат?
- С помощью чертежа раскройте понятия «астрономическая широта» и «астрономическая долгота».
- На какой поверхности определяют положение точек в геодезической системе координат?
- С помощью чертежа раскройте понятия «геодезическая широта» и «геодезическая долгота».
- Почему для повышения точности определения долготы необходимо соединить прямыми линиями ближайшие к точке одноименные десятисекундные деления?
- Как можно рассчитать широту точки, если определить количество минут и секунд от северной рамки топографической карты?
- Какие координаты называют полярными?
- Для каких целей в полярной системе координат служит полярная ось?
- Какие координаты называют биполярными?
- В чем сущность прямой геодезической задачи?
- В чем сущность обратной геодезической задачи?
- Какую величину называют приращением координат?
- Дайте определения синуса, косинуса, тангенса и котангенса угла.
- Как можно применить в топографии теорему Пифагора о соотношении между сторонами прямоугольного треугольника?
- Какую величину называют высотой точки?
- Раскройте понятия: «абсолютная высота точки», «относительная высота точки».
- Как рассчитать абсолютную высоту второй точки, если известны абсолютная высота первой точки и превышение второй точки над первой?
- Какую уровенную поверхность принято считать началом отсчета абсолютных высот в Украине?
- Как называют численное значение высоты?
Определение координат
Предлагаем воспользоваться аналогичным сервисом от Google — найти месторасположение и поиск по координатам + местонахождение интересных мест в мире на схеме Гугл Мапс
Определение широты и долготы на карте?
На странице быстрое определение координат на карте — узнаем широту и долготу города. Онлайн поиск улиц и домов по адресу, по GPS, для определения координат на карте Яндекс, как найти местоположение — подробнее описано ниже.
Определение географических координат любого города в мире (узнать широту и долготу) по онлайн карте от сервиса Яндекс на самом деле очень простой процесс. У вас два удобных варианта, остановимся подробнее на каждом из них.
Вы можете установить приложение для браузера Google Chrome, Opera и Яндекс браузер
Первый вариант: Необходимо воспользоваться формой поиска, и ввести в поле название географического объекта (страну, город, улицу, номер дома). То есть, заполнить форму адресом объекта для нахождения координат. Например, нужно определить географические координаты широту и долготу улиц города Ростова-на-Дону.
Заполняем форму: Ростов-на-Дону Пушкинская 10 (с помощью и при наличии номера дома, поиск будет проходить более точный). Справа в верхнем углу расположена форма определения координат, которая содержит 3 точных параметра — координаты метки, центр карты и масштаб приближения.
После активации поиска «Найти» в каждом поле будут нужные данные — долгота и широта. Смотрим поле «Центр карты».
Второй вариант: В этом случае еще проще. Интерактивная карта мира с координатами содержит метку. По умолчанию она стоит в центре города Москва. Необходимо перетащить метку и поставить на нужный город, например, определяем координаты на карте Санкт-Петербурга с улицами и номерами домов. Широта и долгота автоматически будут соответствовать объекту поиска. Смотрим поле «Координаты метки».
При поиске нужного города или страны, используйте инструменты навигации и масштабирования. Приближая и уменьшая масштаб +/- , также перемещая саму интерактивную карту, легко найти любую страну, искать регион на карте мира. Таким образом, вы можете найти географический центр Украины или России. В стране Украина это поселок Добровеличковка, который расположен на реке Добрая Кировоградская область.
Скопировать географические координаты центра Украины пгт. Добровеличковка — Ctrl+C
48.3848,31.1769 48.3848 северной широты и 31.1769 восточной долготы
Долгота +37° 17′ 6.97″ в.д. (37.1769)
Широта +48° 38′ 4.89″ с.ш. (48.3848)
На въезде в поселок городского типа установлен знак, оповещающий об этом интересном факте. Рассматривать его территорию, скорее всего будет неинтересно. Есть куда более занимательные места в мире.
Как по координатам найти место на карте?
Рассмотрим обратный процесс, для примера сравните определение географических координат широты и долготы по адресу на карте Google. Зачем нужно определение широты и долготы на карте? Допустим вам понадобится, определить по координатам GPS навигатора точное расположение автомобиля на схеме. Или близкий друг позвонит в выходной день и сообщит координаты своего местонахождения, приглашая вас присоединиться к охоте или рыбной ловле.
Зная точные географические координаты, вам пригодится карта с широтой и долготой. Достаточно ввести в форму поиска от сервиса Яндекс свои данные, чтобы определение местоположения по координатам успешно свершилось. Пример, вводим широту и долготу улицы Московская 66 в городе Саратов – 51.5339,46.0368. Сервис быстро определит и покажет в виде метки местоположение данного дома в городе.
Кроме вышеперечисленного, вы легко сможете определить координаты на карте любой станции метро в городе. После названия города пишем название станции. И наблюдаем, где расположится метка и её координаты с широтой и долготой. Для определения протяженности маршрута, необходимо применить инструмент «Линейка» (измерение расстояний на карте). Ставим метку в начале маршрута и затем в конечной точке. Сервис автоматически определит расстояние в метрах и покажет сам трек на карте.
Точнее обследовать место на карте представляется возможным благодаря схеме «Спутник» (верхний угол справа). Посмотрите, как выглядит карта города Новосибирска со спутника. Вы можете проделать с ней все вышеперечисленные операции.
Карта мира с долготой и широтой
Представьте, вы находитесь в незнакомой местности, и рядом нет никаких объектов или ориентиров. И спросить не у кого! Каким образом вы смогли бы объяснить своё точное местоположение, что бы вас быстро нашли?
Благодаря таким понятиям, как широта и долгота, вас смогут обнаружить и найти. Широта показывает местоположение объекта по отношению к Южному и Северному полюсам. За нулевую широту принято считать экватор. Южный полюс расположен на 90 град. южной широты, а Северный на 90 градусе северной широты.
Этих данных оказывается недостаточно. Необходимо знать положение также относительно Востока и Запада. Здесь и пригодится координата долгота.
Сохранить в закладки в любом браузере — CTRL+D
Приглашаем поделиться страницей сервиса со своими друзьями!
Благодарим за предоставленные данные сервис Яндекс. Карты
Географические координаты Москвы на карте планеты: широта и долгота
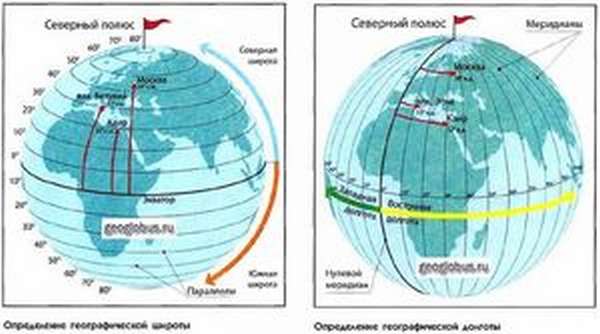Любой объект на Земле имеет свои координаты. Если вспомнить школьный курс географии, то карта представляется своеобразной сеткой. Параллельные линии этой сетки называются параллелями, а вертикальные — меридианами. По пересечению этих линий легко определяется местоположение любого населённого пункта. Параллель всегда соответствует широте. Санкт-Петербург находится на 60-й параллели, значит, в координатах указывается 60 северной широты (с.ш.). Аналогично надо работать и с меридианами.
- Географические координаты Москвы
- Широта и долгота
- Определение координат в повседневной жизни
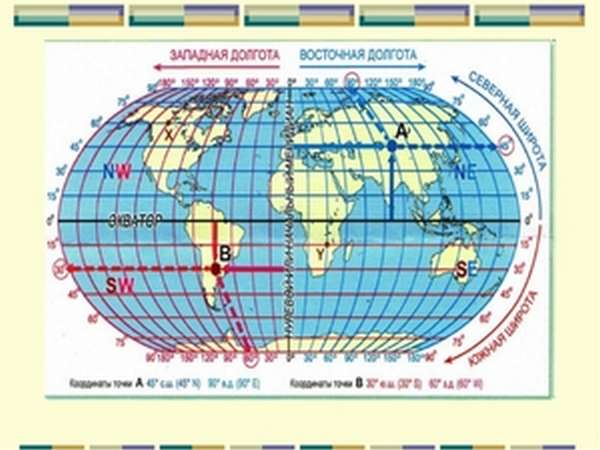В официальных документах под широтой понимается угол от точки зенита и плоскости экватора. Экватор принято считать нулевой параллелью, от которой на север и на юг отходят другие, заканчиваясь на полюсах (90).
Меридианом называют линию, проведённую через любую точку на поверхности Земли и проходящую через земную ось. Исчисления ведутся от нулевого меридиана. Все меридианы расходятся от нулевого на запад и на восток до пределов 180. Меридианы могут пересекаться на полюсах планеты.
Географические координаты Москвы
Москва занимает удобное положение. Располагаясь на семи холмах и между двух рек, она находится на высоте 145 метров над уровнем моря. Считается, что параллель, на которой она стоит, является «золотой». На самом деле на «золотой параллели» находится Крымский полуостров, а Москва на «золотом сечении».
Это интересно: что является непосредственной причиной возникновения поясов атмосферного давления?
Разница в том, что «золотая параллель» является своеобразным центром Земли, а «золотое сечение» — центром Северного полушария и нашей страны. На той же самой параллели располагаются много городов как внутри России, так и за её пределами. «Золотое сечение» является самым гармоничным местом на Земле для развития и существования человечества. Однако в Южном полушарии это самое безлюдное место.
Широта и долгота
Так как столица существует много веков, то исторически и благодаря сечению это место является наиболее выгодным в экономическом смысле. После того как город стал столицей, он соединил международные пути с Запада на Восток и обратно. Первоначально это были караванные пути. Позже связь с другими странами стала железнодорожной и воздушной. Сегодня Москва является важным транспортным узлом, из которого можно добраться в любую точку Европы всего за 1−2 часа (в зависимости от транспорта). Современный транспорт устроен так, что в его компьютерах забиты так называемые географические адреса пунктов назначения.
Это интересно: связь современной географии с другими науками.
Простому человеку забивать голову ненужной информацией не нужно, достаточно иметь об этом общее представление. Знание о том, по какому адресу следует искать главный город России, никому не повредит и может пригодиться в какой-нибудь нестандартной ситуации.
Если навскидку задать кому-нибудь вопрос о том, где находится Москва, то ответы будут примерно такого рода:
- в России,
- в Северном полушарии,
- на 55-й параллели.
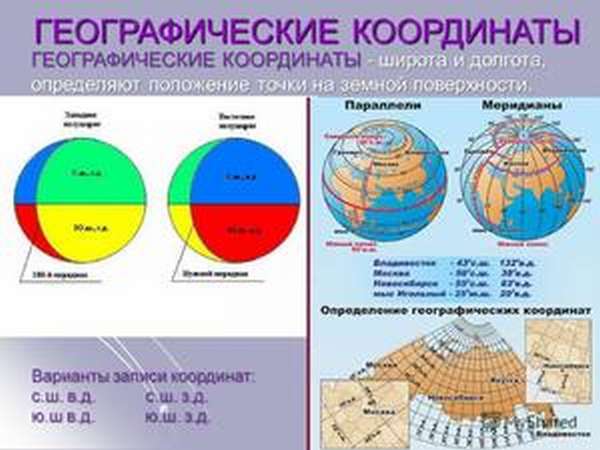Так как широта напрямую зависит от экватора, то вверх от него она будет называться северной, а вниз — южной. В случае с третьим ответом как раз применим принцип, что адрес данного объекта равен 55 северной широты (с.ш.), так как мы всё же живём выше от экватора. Но это только половина адреса. Следуя принятой системе координат, необходимо определить, с какой стороны от нулевого меридиана находится определяемое место. Так как нулевой меридиан расположен в Англии, то вторая часть адреса будет такой — 37 восточной долготы.
Географические адреса какой-либо точки на местности вычисляются двумя известными способами: DD и DMS. В отношении Москвы это будет выглядеть так:
- по десятичной системе (DD) — 55.753960×37.620393,
- система градусов, минут и секунд (DMS) — 554520.974″ с. ш., 37372.279″ в. д.
В основном применяется система DD.
Определение координат в повседневной жизни
Если раньше необходимость в определении местоположения объектов была только у некоторых специализированных профессий, то теперь все мы используем это, не задумываясь. Возможно, не все это знают и будут весьма удивлены такому факту. У всех нас есть компьютеры и телефоны, в которых встроена функция отслеживания местоположения. При наличии интернета и включенной функции Гугл или Яндекс автоматически определяют, где мы находимся, и даже прокладывают путь по карте.
- Те самые GPS координаты, а теперь и ГЛОНАСС базируются именно на десятичной системе (DD). Достаточно написать населённый пункт в поисковой строке, и по заложенной в программу базе координат система позиционирования тут же выдаст искомое.
- Можно осуществлять поиск и по координатам (DMS). Для этого в поисковой строке вбиваем 55450N 37370E. Таким образом, Москва будет найдена по указанным цифрам.
- Определить координаты позволяют и многочисленные справочники. Если же есть желание, например, узнать свои координаты, нужно на открытой карте в электронном устройстве кликнуть левой кнопкой мышки туда, где вы находитесь. Система тут же выдаст подобный набор цифр в формате DMS.
Географические координаты Ульяновска (широта и долгота)
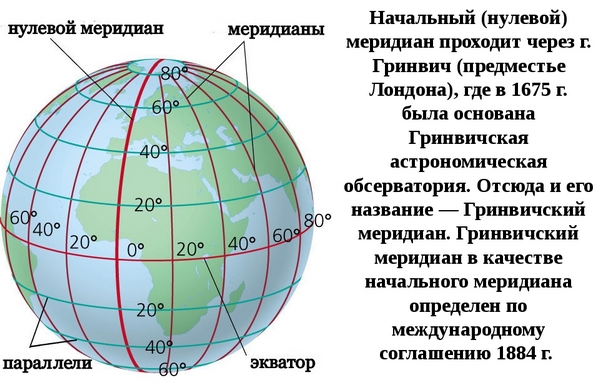
Градусная сеть Земли – система меридианов и параллелей на географических картах и глобусах, служащая для отсчета географических координат точек земной поверхности – долгот и широт – или нанесения на карту объектов по их координатам.
Для создания градусной сети необходимы определенные точки отсчета. Шарообразная форма Земли определяет существование на земной поверхности двух неподвижных точек – полюсов. Через полюсы проходит воображаемая ось, вокруг которой вращается Земля.
Основные элементы градусной сетки карты — полюсы, экватор, меридианы и параллели.
Географические полюсы – математически высчитанные точки пересечения воображаемой оси вращения Земли с земной поверхностью.
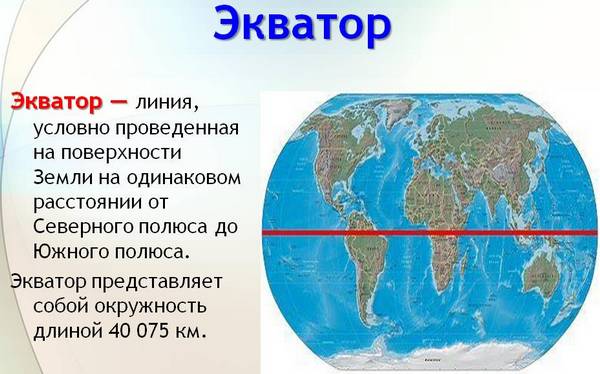
Экватор – воображаемая линия на земной поверхности, полученная при мысленном рассечении эллипсоида на две равные части (Северное и Южное полушарие).
Все точки экватора равноудалены от полюсов. Плоскость экватора перпендикулярна оси вращения Земли и проходит через ее центр. Полушария мысленно разделены еще множеством плоскостей, параллельных плоскости экватора.
Линии их пересечения с поверхностью эллипсоида называются параллелями .
Все они, как и плоскость экватора, перпендикулярны оси вращения планеты. Параллелей на карте и глобусе можно провести сколько угодно, но обычно на учебных картах их проводят с интервалом 10—20°. Параллели всегда ориентированы с запада на восток. Длина окружности параллелей уменьшается от экватора к полюсам. На экваторе она самая большая, а на полюсах равна нулю.
При пересечении земного шара воображаемыми плоскостями, проходящими через ось Земли перпендикулярно плоскости экватора, образуются большие окружности – меридианы .
Меридианы также можно провести через любые точки эллипсоида. Все они пересекаются в точках полюсов. Меридианы ориентированы с севера на юг. Средняя длина дуги 1° меридиана: 40 008,5 км : 360° = 111 км. Длина всех меридианов одинакова. Направление местного меридиана в любой точке можно определить в полдень по тени от любого предмета. В Северном полушарии конец тени всегда показывает направление на север, в Южном – на юг.
Градусная сеть необходима для отсчета географических координат точек земной поверхности – широты и долготы.
Географические координаты.
Географические координаты — это географическая широта и долгота.
Географическая широта – расстояние вдоль меридиана в градусах от экватора до какой-либо точки на поверхности Земли.
Началом отсчета является экватор. Широта всех точек на нем равна 0. На полюсах широта составляет 90°. К северу от экватора отсчитывают северную широту, к югу – южную.
Географическая долгота – расстояние вдоль параллели в градусах от начального меридиана до какой-либо точки земной поверхности.
Все меридианы равны по длине, поэтому для отсчета необходимо было выбрать один из них. Им стал Гринвичский меридиан, проходящий недалеко от Лондона (там, где расположена Гринвичская обсерватория). Долгота отсчитывается от 0° до 180°. К востоку от нулевого меридиана до 180° отсчитывается восточная долгота, к западу – западная. Таким образом, используя градусную сеть, можно точно определить географические координаты – величины, определяющие положение точки на земной поверхности относительно экватора и нулевого меридиана.
Например, географические координаты мыса Челюскин (крайней северной точки Евразии) – 78° с. ш. и 104° в. д.
Глобус
Глобус (от лат. globus, «шар») — это обобщенная модель Земли [или другой планеты, а также модель небесной сферы (небесный глобус)], приведённая из её реальной формы к упрощенной и уменьшенной форме сферы. Обычно на глобусах в уменьшенном виде изображают поверхность Земли: очертания суши и водных объектов, рельеф материков и дна Мирового океана, реки, а также границы государств, города.
Глобус наиболее точно отражает облик Земли. Глобус обладает целым рядом геометрических свойств:
- равномасштабность изображения — любой отрезок линии на поверхности земного шара изображается на глобусе с одинаковым уменьшением, т. е. его масштаб всюду постоянен;
- равноугольность — горизонтальные углы, измеренные на земной поверхности, равны соответствующим углам на глобусе, а изображение любого географического объекта на глобусе подобно его действительным очертаниям на местности;
- равновеликость — глобус сохраняет правильное соотношение площадей.
На глобусе правильно переданы очертания, размеры, взаимное расположение материков и океанов. Есть и другие отличия глобуса от географической карты.
Закрепить теорию практикой !
(пройти тесты с проверкой ответа сразу и объяснением правильного ответа)
Географические координаты Ульяновска (широта и долгота)
Градусная сеть Земли – система меридианов и параллелей на географических картах и глобусах, служащая для отсчета географических координат точек земной поверхности – долгот и широт – или нанесения на карту объектов по их координатам.
Для создания градусной сети необходимы определенные точки отсчета. Шарообразная форма Земли определяет существование на земной поверхности двух неподвижных точек – полюсов. Через полюсы проходит воображаемая ось, вокруг которой вращается Земля.
Основные элементы градусной сетки карты — полюсы, экватор, меридианы и параллели.
Географические полюсы – математически высчитанные точки пересечения воображаемой оси вращения Земли с земной поверхностью.
Экватор – воображаемая линия на земной поверхности, полученная при мысленном рассечении эллипсоида на две равные части (Северное и Южное полушарие).
Все точки экватора равноудалены от полюсов. Плоскость экватора перпендикулярна оси вращения Земли и проходит через ее центр. Полушария мысленно разделены еще множеством плоскостей, параллельных плоскости экватора.
Линии их пересечения с поверхностью эллипсоида называются параллелями .
Все они, как и плоскость экватора, перпендикулярны оси вращения планеты. Параллелей на карте и глобусе можно провести сколько угодно, но обычно на учебных картах их проводят с интервалом 10—20°. Параллели всегда ориентированы с запада на восток. Длина окружности параллелей уменьшается от экватора к полюсам. На экваторе она самая большая, а на полюсах равна нулю.
При пересечении земного шара воображаемыми плоскостями, проходящими через ось Земли перпендикулярно плоскости экватора, образуются большие окружности – меридианы .
Меридианы также можно провести через любые точки эллипсоида. Все они пересекаются в точках полюсов. Меридианы ориентированы с севера на юг. Средняя длина дуги 1° меридиана: 40 008,5 км : 360° = 111 км. Длина всех меридианов одинакова. Направление местного меридиана в любой точке можно определить в полдень по тени от любого предмета. В Северном полушарии конец тени всегда показывает направление на север, в Южном – на юг.
Градусная сеть необходима для отсчета географических координат точек земной поверхности – широты и долготы.
Географические координаты.
Географические координаты — это географическая широта и долгота.
Географическая широта – расстояние вдоль меридиана в градусах от экватора до какой-либо точки на поверхности Земли.
Началом отсчета является экватор. Широта всех точек на нем равна 0. На полюсах широта составляет 90°. К северу от экватора отсчитывают северную широту, к югу – южную.
Географическая долгота – расстояние вдоль параллели в градусах от начального меридиана до какой-либо точки земной поверхности.
Все меридианы равны по длине, поэтому для отсчета необходимо было выбрать один из них. Им стал Гринвичский меридиан, проходящий недалеко от Лондона (там, где расположена Гринвичская обсерватория). Долгота отсчитывается от 0° до 180°. К востоку от нулевого меридиана до 180° отсчитывается восточная долгота, к западу – западная. Таким образом, используя градусную сеть, можно точно определить географические координаты – величины, определяющие положение точки на земной поверхности относительно экватора и нулевого меридиана.
Например, географические координаты мыса Челюскин (крайней северной точки Евразии) – 78° с. ш. и 104° в. д.
Глобус
Глобус (от лат. globus, «шар») — это обобщенная модель Земли [или другой планеты, а также модель небесной сферы (небесный глобус)], приведённая из её реальной формы к упрощенной и уменьшенной форме сферы. Обычно на глобусах в уменьшенном виде изображают поверхность Земли: очертания суши и водных объектов, рельеф материков и дна Мирового океана, реки, а также границы государств, города.
Глобус наиболее точно отражает облик Земли. Глобус обладает целым рядом геометрических свойств:
- равномасштабность изображения — любой отрезок линии на поверхности земного шара изображается на глобусе с одинаковым уменьшением, т. е. его масштаб всюду постоянен;
- равноугольность — горизонтальные углы, измеренные на земной поверхности, равны соответствующим углам на глобусе, а изображение любого географического объекта на глобусе подобно его действительным очертаниям на местности;
- равновеликость — глобус сохраняет правильное соотношение площадей.
На глобусе правильно переданы очертания, размеры, взаимное расположение материков и океанов. Есть и другие отличия глобуса от географической карты.
Закрепить теорию практикой !
(пройти тесты с проверкой ответа сразу и объяснением правильного ответа)
Географические координаты
Географи́ческие координа́ты — обобщённое понятие о геодезических и астрономических координатах, когда уклонение отвесной линии не учитывают [1] . Иными словами, при определении географических координат Земля принимается за шар. Географические координаты определяют положение точки на земной поверхности или, более широко, в географической оболочке. Географические координаты строятся по принципу сферических. Аналогичные координаты применяются для других планет, а также на небесной сфере [2] .
Широта́ — угол φ между местным направлением зенита и плоскостью экватора, отсчитываемый от 0° до 90° в обе стороны от экватора. Географическую широту точек, лежащих в северном полушарии, (северную широту) принято считать положительной, широту точек в южном полушарии — отрицательной. О широтах, близких к полюсам, принято говорить как о высоких, а о близких к экватору — как о низких.
Из-за отличия формы Земли от шара, географическая широта точек несколько отличается от их геоцентрической широты, то есть от угла между направлением на данную точку из центра Земли и плоскостью экватора.
Широту места можно определить с помощью таких астрономических инструментов, как секстант или гномон (прямое измерение), также можно воспользоваться системами GPS или ГЛОНАСС (косвенное измерение).
Долгота́ — двугранный угол λ между плоскостью меридиана, проходящего через данную точку, и плоскостью начального нулевого меридиана, от которого ведётся отсчёт долготы. Долготу от 0° до 180° к востоку от нулевого меридиана называют восточной, к западу — западной. Восточные долготы принято считать положительными, западные — отрицательными.
Выбор нулевого меридиана произволен и зависит только от соглашения. Сейчас за нулевой меридиан принят Опорный меридиан, проходящий рядом с обсерваторией в Гринвиче, на юго-востоке Лондона. В качестве нулевого ранее выбирались меридианы обсерваторий Парижа, Кадиса, Пулкова и т. д.
Чтобы полностью определить положение точки трёхмерного пространства, необходима третья координата — высота. Расстояние до центра планеты не используется в географии: оно удобно лишь при описании очень глубоких областей планеты или, напротив, при расчёте орбит в космосе.
В пределах географической оболочки применяется обычно высота над уровнем моря, отсчитываемая от уровня «сглаженной» поверхности — геоида. Такая система трёх координат оказывается ортогональной, что упрощает ряд вычислений. Высота над уровнем моря удобна ещё тем, что связана с атмосферным давлением.
Расстояние от земной поверхности (ввысь или вглубь) часто используется для описания места, однако ‘не’ служит координатой.
В навигации в качестве начала системы координат выбирается центр масс транспортного средства (ТС). Переход начала координат из инерциальной системы координат в географическую (то есть из O i 
в O g ) осуществляется исходя из значений широты и долготы. Координаты центра географической системы координат O g в инерциальной принимают значения (при расчёте по шарообразной модели Земли):
X o g = ( R + h ) cos ( φ ) cos ( U t + λ ) Y o g = ( R + h ) cos ( φ ) sin ( U t + λ ) Z o g = ( R + h ) sin ( φ ) где R — радиус земли , U — угловая скорость вращения Земли, h — высота над уровнем моря, φ — широта, λ — долгота, t — время.
Ориентация осей в географической системе координат (Г. С. К.) выбирается по схеме:
Ось X (другое обозначение — ось E) — ось, направленная на восток. Ось Y (другое обозначение — ось N) — ось, направленная на север. Ось Z (другое обозначение — ось Up) — ось, направленная вертикально вверх.
Ориентация трёхгранника XYZ,из-за вращения земли и движения Т. С. постоянно смещается с угловыми скоростями [3] .
ω E = − V N / R ω N = V E / R + U cos ( φ ) ω U p = V E R t g ( φ ) + U sin ( φ ) где R — радиус земли , U — угловая скорость вращения Земли, V N — скорость транспортного средства на север, V E — на восток, φ — широта, λ — долгота.
Основным недостатком в практическом применении Г. С. К. в навигации является большие величины угловой скорости этой системы в высоких широтах, возрастающие вплоть до бесконечности на полюсе. Поэтому вместо Г. С. К. используется полусвободная в азимуте СК.
Полусвободная в азимуте система координат
Полусвободная в азимуте С. К. отличается от Г. С. К. только одним уравнением, которое имеет вид:
ω U p = U sin ( φ )
Соответственно, система имеет тоже начальное положение, осуществляется по формуле [3]
N = Y w cos ( ε ) + X w sin ( ε ) E = − Y w sin ( ε ) + X w cos ( ε )
В реальности все расчёты ведутся именно в этой системе, а потом, для выдачи выходной информации происходит преобразование координат в ГСК.
Для записи географических координат может использоваться любой эллипсоид (или геоид), но чаще всего используются WGS 84 и Красовского (на территории РФ).
Координаты (широта от −90° до +90°, долгота от −180° до +180°) могут записываться:
- в ° градусах в виде десятичной дроби (современный вариант)
- в ° градусах и ′ минутах с десятичной дробью
- в ° градусах, ′ минутах и ″ секундах с десятичной дробью (исторически сложившаяся форма записи)
Разделителем десятичной дроби может служить точка или запятая. Положительные знаки координат представляются (в большинстве случаев опускаемым) знаком «+» либо буквами:
- «N» или «с. ш.» — северная широта,
- «E» или «в. д.» — восточная долгота.
Отрицательные знаки координат представляются либо знаком «−», либо буквами:
- «S» или «ю. ш.» — южная широта,
- «W» или «з. д.» — западная долгота.
Буквы могут стоять как впереди, так и сзади. Единых правил записи координат не существует.
На картах поисковых систем по умолчанию показываются координаты в градусах с десятичной дробью со знаком «−» для отрицательной долготы. На картах Google и картах Яндекс вначале широта, затем долгота (до октября 2012 на картах Яндекс был принят обратный порядок: сначала долгота, потом широта). Эти координаты видны, например, при прокладке маршрутов от произвольных точек. При поиске распознаются и другие форматы.
В то же время часто используется и исконный способ записи с градусами, минутами и секундами. В настоящее время координаты могут записываться одним из множества способов или дублироваться двумя основными (с градусами и с градусами, минутами и секундами) [4] . Как пример, варианты записи координат знака «Нулевой километр автодорог Российской Федерации» — 55°45′21″ с. ш. 37°37′04″ в. д. H G Я O L :
- 55,755831°, 37,617673° — градусы
- N55.755831°, E37.617673° — градусы (+ доп. буквы)
- 55°45.35′N, 37°37.06′E — градусы и минуты (+ доп. буквы)
- 55°45′20.9916″N, 37°37′3.6228″E — градусы, минуты и секунды (+ доп. буквы)
При необходимости форматы можно пересчитать самостоятельно: 1° = 60′ (минутам), 1′ (минута) = 60″ (секундам). Также можно использовать специализированные сервисы. См. ссылки.
Загрузка...